ОпределенияСначала напомним некоторые определения из лекции 1. Орграфом  называется
пара называется
пара 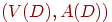 , где , где  непустое
конечное множество элементов, называемых вершинами, а непустое
конечное множество элементов, называемых вершинами, а 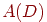 —
конечное семейство упорядоченных пар элементов из —
конечное семейство упорядоченных пар элементов из  ,
называемых дугами (или
ориентированными ребрами). Дуга, у которой
вершина ,
называемых дугами (или
ориентированными ребрами). Дуга, у которой
вершина  является первым элементом, а вершина является первым элементом, а вершина  — вторым, называется дугой
из
— вторым, называется дугой
из  в в  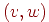 . Заметим, что
дуги . Заметим, что
дуги 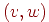 и и 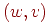 различны. Хотя графы и орграфы
— различные объекты, в определенных случаях графы можно рассматривать как орграфы, в
которых каждому ребру соответствуют две противоположно ориентированные
дуги. различны. Хотя графы и орграфы
— различные объекты, в определенных случаях графы можно рассматривать как орграфы, в
которых каждому ребру соответствуют две противоположно ориентированные
дуги.  и и  называются соответственно
множеством вершин и семейством дуг орграфа называются соответственно
множеством вершин и семейством дуг орграфа  . . 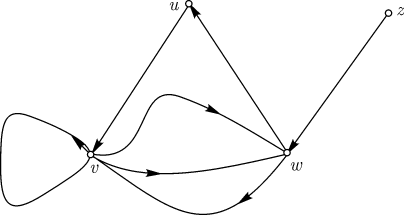
Рис. 9.1.
На (рис. 9.1) представлен орграф, дугами которого являются
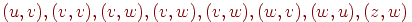 . Порядок вершин
на дуге указан стрелкой. Граф, полученный из орграфа . Порядок вершин
на дуге указан стрелкой. Граф, полученный из орграфа  удалением
стрелок, то есть заменой каждой дуги вида удалением
стрелок, то есть заменой каждой дуги вида 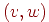 на соответствующее ребро на соответствующее ребро
 , называется основанием орграфа , называется основанием орграфа  . Многие
определения, данные для графов, можно перенести на орграфы. К примеру, две вершины . Многие
определения, данные для графов, можно перенести на орграфы. К примеру, две вершины
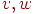 орграфа орграфа  называются смежными, если в называются смежными, если в 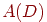 существует
дуга вида существует
дуга вида 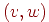 или или 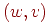 ; при этом
вершины ; при этом
вершины 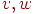 называются
инцидентными любой такой дуге (а дуга — инцидентной соответствующим
вершинам). Два орграфа называются изоморфными, если
существует изоморфизм между их основаниями, сохраняющий порядок вершин на
каждой дуге. Матрицей смежности орграфа с множеством вершин называются
инцидентными любой такой дуге (а дуга — инцидентной соответствующим
вершинам). Два орграфа называются изоморфными, если
существует изоморфизм между их основаниями, сохраняющий порядок вершин на
каждой дуге. Матрицей смежности орграфа с множеством вершин  является матрица, в которой является матрица, в которой  равно числу дуг
вида равно числу дуг
вида 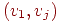 в семействе в семействе 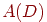 . Матрица
смежности для начерченного графа . Матрица
смежности для начерченного графа 
Орграфы , не
содержащие петель и кратных ребер, называются простыми. Ориентированный маршрут
в орграфе  представляет собой конечную последовательность дуг вида представляет собой конечную последовательность дуг вида
 . Эту
последовательность можно записывать в виде . Эту
последовательность можно записывать в виде  и говорить об ориентированном маршруте из
и говорить об ориентированном маршруте из  в в  .
Аналогичным образом можно определить ориентированные цепи, ориентированные простые цепи и
ориентированные циклы — орцепи, простые орцепи и орциклы.
Заметим, что хотя орцепь не может содержать данную дугу .
Аналогичным образом можно определить ориентированные цепи, ориентированные простые цепи и
ориентированные циклы — орцепи, простые орцепи и орциклы.
Заметим, что хотя орцепь не может содержать данную дугу 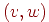 более одного раза, она может содержать одновременно
более одного раза, она может содержать одновременно 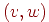 и
и 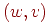 .
Например, на (рис. 9.1) .
Например, на (рис. 9.1)  является орцепью. является орцепью. Определим два наиболее естественных и полезных типа связности орграфов,
которые возникают в соответствии с тем, хотим мы или нет принимать во
внимание ориентацию дуг. Говорят, что орграф  связен,
или слабо связен, если он не может быть представлен в виде
объединения двух различных орграфов (определенных обычным образом). Это эквивалентно
тому, что связно основание орграфа связен,
или слабо связен, если он не может быть представлен в виде
объединения двух различных орграфов (определенных обычным образом). Это эквивалентно
тому, что связно основание орграфа  . Предположим также, что для
любых двух вершин . Предположим также, что для
любых двух вершин 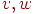 орграфа орграфа  существует простая орцепь
из существует простая орцепь
из  в в  ,
тогда ,
тогда  называется сильно связным. Этот термин настолько
устоялся, что мы использовали его вместо более естественного " орсвязный ". Ясно, что любой сильно связный граф связен, но
обратное неверно. На (рис. 9.1) изображен связный орграф, не являющийся сильно
связным, так как не существует простой орцепи из называется сильно связным. Этот термин настолько
устоялся, что мы использовали его вместо более естественного " орсвязный ". Ясно, что любой сильно связный граф связен, но
обратное неверно. На (рис. 9.1) изображен связный орграф, не являющийся сильно
связным, так как не существует простой орцепи из  в
в  . . Различие между связным и сильно связным орграфом станет яснее, если
рассмотреть план города, по всем улицам которого допускается только
одностороннее движение. Тогда связность соответствующего орграфа означает,
что можно проехать из любой части города в любую другую, не
обращая внимания на правила одностороннего движения. Если же этот орграф
сильно связан, то можно проехать из любой части города в любую другую, следуя
всегда "правильным путем" вдоль улиц с односторонним движением. Важно, чтобы система с односторонним движением была сильно связной, и
естественно возникает вопрос: при каких условиях карту улиц можно
превратить в систему с односторонним движением таким способом, чтобы можно
было проехать из любой части города в любую другую? Если, к примеру, город
состоит из двух частей, связанных одним мостом, то мы никогда не сможем
сделать все его улицы односторонними, поскольку какое бы направление ни
приписали мосту, одна часть города будет отрезана. Сюда включается и тот
случай, когда в городе имеется тупик. С другой стороны, если мостов нет,
то всегда найдется подходящая односторонняя система; это и есть основной
результат, который будет установлен ниже в теореме. Для удобства будем называть граф  ориентируемым, если каждое
его ребро (рассматриваемое как пара вершин) может быть упорядочено таким
образом, что полученный в результате орграф будет сильно связным. Этот
процесс упорядочивания ребер будем называть заданием ориентации
графа или приписыванием направлений ребрам.
Если, например, ориентируемым, если каждое
его ребро (рассматриваемое как пара вершин) может быть упорядочено таким
образом, что полученный в результате орграф будет сильно связным. Этот
процесс упорядочивания ребер будем называть заданием ориентации
графа или приписыванием направлений ребрам.
Если, например,  — граф, изображенный на (рис. 9.2), то его можно
ориентировать и получить сильно связный орграф, изображенный на (рис. 9.3). — граф, изображенный на (рис. 9.2), то его можно
ориентировать и получить сильно связный орграф, изображенный на (рис. 9.3). 
Рис. 9.2.
| | 
Рис. 9.3.
|
Мы видим, что любой эйлеров граф ориентируем, поскольку достаточно пройти
по любой эйлеровой цепи, ориентируя ребра в направлении движения по ним.
Дадим необходимое и достаточное условие ориентируемого графа. Теорема 9.1 (Роббинс)
Пусть  — связный граф; он ориентируем тогда и только
тогда, если каждое его ребро содержится, по крайней мере, в одном цикле. — связный граф; он ориентируем тогда и только
тогда, если каждое его ребро содержится, по крайней мере, в одном цикле.
ДоказательствоНеобходимость условия очевидна. Чтобы доказать достаточность,
выберем любой цикл  и ориентируем его ребра в направлении
какого-либо обхода этого цикла. Если каждое ребро из и ориентируем его ребра в направлении
какого-либо обхода этого цикла. Если каждое ребро из  содержится
в содержится
в  , то доказательство завершено; если нет, то возьмем любое ребро , то доказательство завершено; если нет, то возьмем любое ребро  , не
принадлежащее , не
принадлежащее  , но смежное некоторому ребру из , но смежное некоторому ребру из  .
По предположению, ребро .
По предположению, ребро  содержится в каком-то цикле содержится в каком-то цикле  . Ребрам
цикла . Ребрам
цикла  можно приписать ориентацию в направлении какого-либо обхода этого цикла
(за исключением тех ребер, которые уже были ориентированы, то есть тех
ребер из можно приписать ориентацию в направлении какого-либо обхода этого цикла
(за исключением тех ребер, которые уже были ориентированы, то есть тех
ребер из  , которые принадлежат также , которые принадлежат также  ).
Нетрудно убедиться в
том, что описанная процедура за конечное число шагов приведет к сильно
связному орграфу. ).
Нетрудно убедиться в
том, что описанная процедура за конечное число шагов приведет к сильно
связному орграфу. Эйлеровы и гамильтоновы орграфыСвязный
орграф  называется эйлеровым, если в нем
существует замкнутая орцепь, содержащая каждую его дугу. Такая орцепь называется эйлеровой орцепью. называется эйлеровым, если в нем
существует замкнутая орцепь, содержащая каждую его дугу. Такая орцепь называется эйлеровой орцепью. Например, граф, изображенный на рисунке, не является эйлеровым, хотя его
основание — эйлеров граф. 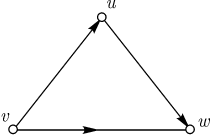
Рис. 9.4.
Наша первая задача — найти условие, необходимое и достаточное для
того, чтобы связный орграф был эйлеровым. Очевидно, что необходимым условием
эйлеровости орграфа является его сильная связь. Если  —
вершина орграфа —
вершина орграфа
 , то называют полустепенью исхода , то называют полустепенью исхода  (обозначается
(обозначается  — стрелка направлена
от — стрелка направлена
от  ) число
дуг орграфа ) число
дуг орграфа  , имеющих вид , имеющих вид 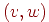 . Аналогично,
полустепенью захода . Аналогично,
полустепенью захода  (обозначается
(обозначается  называется
число дуг из называется
число дуг из  вида вида 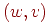 . Отсюда сразу следует, что сумма
полустепеней
захода всех вершин орграфа . Отсюда сразу следует, что сумма
полустепеней
захода всех вершин орграфа  равна сумме их
полустепеней исхода, поскольку каждая дуга из равна сумме их
полустепеней исхода, поскольку каждая дуга из  участвует в каждой сумме ровно один
раз. Будем называть этот результат орлемой о рукопожатиях! участвует в каждой сумме ровно один
раз. Будем называть этот результат орлемой о рукопожатиях! Источником
орграфа  называют вершину, у которой полустепень
захода равна нулю. Стоком орграфа называют вершину, у которой полустепень
захода равна нулю. Стоком орграфа  называют
вершину, у которой полустепень исхода равна нулю. Так, на (рис. 9.4) вершина называют
вершину, у которой полустепень исхода равна нулю. Так, на (рис. 9.4) вершина  является
источником, а является
источником, а  — стоком. Заметим, что эйлеров орграф, кроме
тривиального орграфа, не содержащего дуг, не может иметь ни источников,
ни стоков. — стоком. Заметим, что эйлеров орграф, кроме
тривиального орграфа, не содержащего дуг, не может иметь ни источников,
ни стоков. Теорема 9.2.
Связный орграф является эйлеровым тогда и только тогда, если
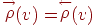 для каждой его вершины
для каждой его вершины  . .
Теорема дается без доказательства, так как оно аналогично тем, которые
даны в лекции 4.
Орграф  называется гамильтоновым, если в нем
существует орцикл, включающий каждую его вершину. Орграф, содержащий простую
орцепь, проходящую через каждую вершину, называется
полугамильтоновым. О гамильтоновых орграфах известно очень мало,
к тому же некоторые теоремы о гамильтоновых графах, по-видимому, нелегко, если
вообще возможно, обобщить на орграфы. Естественно спросить: обобщается ли
на орграфы теорема Дирака? Одно такое обобщение принадлежит Гуйя-Ури.
Доказательство этого утверждения значительно сложнее, чем доказательство
теоремы Дирака, и выходит за рамки этого курса. Доказательство теоремы
Гуйя-Ури можно найти в книге C.Berge, Graphs and hypergraphs,
North-Holland, 1973, Р. 196. называется гамильтоновым, если в нем
существует орцикл, включающий каждую его вершину. Орграф, содержащий простую
орцепь, проходящую через каждую вершину, называется
полугамильтоновым. О гамильтоновых орграфах известно очень мало,
к тому же некоторые теоремы о гамильтоновых графах, по-видимому, нелегко, если
вообще возможно, обобщить на орграфы. Естественно спросить: обобщается ли
на орграфы теорема Дирака? Одно такое обобщение принадлежит Гуйя-Ури.
Доказательство этого утверждения значительно сложнее, чем доказательство
теоремы Дирака, и выходит за рамки этого курса. Доказательство теоремы
Гуйя-Ури можно найти в книге C.Berge, Graphs and hypergraphs,
North-Holland, 1973, Р. 196. Теорема (Гуйя-Ури, 1973)
Пусть  — сильно связный орграф,
имеющий — сильно связный орграф,
имеющий  вершин.
Если вершин.
Если  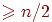 и и
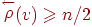 для любой его
вершины для любой его
вершины  , то , то  является гамильтоновым орграфом. является гамильтоновым орграфом.
Кажется, что получать результаты в этом направлении не очень просто,
поэтому ограничимся рассмотрением вопроса о том, какие типы орграфов
являются гамильтоновыми. В этом аспекте широко известен один тип
орграфов — турниры. Для них соответствующие результаты принимают
наиболее простую форму. Турниры
Турниром называется орграф, в котором любые две вершины соединены
ровно одной дугой (см. рис. 9.5). 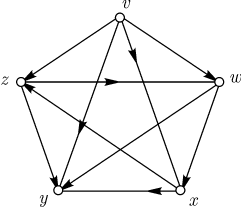
Рис. 9.5.
Основанием для выбора такого названия служит то, что подобные орграфы
можно использовать для записи результатов теннисных или любых других
турниров, в которых не разрешены ничьи. Например, на (рис. 9.5) представлены
результаты турнира, в котором команда  нанесла поражение
команде нанесла поражение
команде  ,
но проиграла команде ,
но проиграла команде  , и т.д. , и т.д. Поскольку турнир может обладать источником или стоком, турниры не являются
в общем случае гамильтоновыми орграфами. Однако следующая теорема
(принадлежащая Реди и Камиону) показывает, что всякий турнир почти
гамильтонов. Теорема 9.3 (Реди, Камион). - Всякий турнир полугамильтонов.
- Всякий сильно связный турнир гамильтонов.
Доказательство 1. Если турнир имеет меньше четырех вершин, то утверждение,
очевидно, верно. Проведем индукцию по числу вершин. Предположим, что любой
турнир с  вершинами полугамильтонов. Пусть вершинами полугамильтонов. Пусть  — турнир с
— турнир с  вершинами, и пусть турнир
вершинами, и пусть турнир  с с  вершинами получен
из вершинами получен
из  удалением
некоторой вершины удалением
некоторой вершины  вместе со всеми инцидентными ей дугами.
Тогда, по предположению индукции, вместе со всеми инцидентными ей дугами.
Тогда, по предположению индукции,  обладает полугамильтоновой простой
орцепью обладает полугамильтоновой простой
орцепью  . Рассмотрим три
случая. . Рассмотрим три
случая. - Если
 — дуга в — дуга в  , то искомой
простой орцепью является , то искомой
простой орцепью является 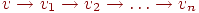 . . - Если
 не является дугой в не является дугой в  , это
означает, что дугой является , это
означает, что дугой является  и если существует такое и если существует такое  , что , что
 — дуга в — дуга в  , то выбирая первое , то выбирая первое  с таким свойством,
получим, что искомой простой орцепью является с таким свойством,
получим, что искомой простой орцепью является  (см. рис. 9.6). (см. рис. 9.6). - Если в
 не существует дуги вида не существует дуги вида 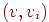 , то
искомой простой орцепью является , то
искомой простой орцепью является  . .
2. Докажем более сильный результат, состоящий в том, что сильно связный
турнир  с с  вершинами содержит орциклы длин вершинами содержит орциклы длин
 . . 
Рис. 9.6.
Сначала покажем, что  содержит орцикл длины три. Для этого
выберем в содержит орцикл длины три. Для этого
выберем в  произвольную вершину произвольную вершину  и обозначим
через и обозначим
через  множество всех
вершин множество всех
вершин  , таких, что , таких, что 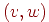 — дуга
в — дуга
в  , а через , а через  —
обозначим множество всех вершин —
обозначим множество всех вершин  , таких, что , таких, что  — дуга в
— дуга в  .
Так как .
Так как  сильно связен, то оба множества сильно связен, то оба множества  и
и  не пусты,
и поэтому в не пусты,
и поэтому в  найдется дуга вида найдется дуга вида 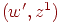 ,
где ,
где  принадлежит
принадлежит  , ,  принадлежит принадлежит  .
Тогда требуемым циклом длины три является .
Тогда требуемым циклом длины три является  . . Осталось только показать, что если существует орцикл длины 
 ,
то существует и орцикл длины ,
то существует и орцикл длины  . Пусть . Пусть  — орцикл длины — орцикл длины  . Предположим сначала, что
в . Предположим сначала, что
в  существует
вершина существует
вершина  , не принадлежащая этому орциклу и обладающая тем
свойством, что в , не принадлежащая этому орциклу и обладающая тем
свойством, что в  содержатся дуги вида содержатся дуги вида 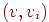 и вида и вида
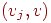 . Тогда должна существовать такая вершина . Тогда должна существовать такая вершина  , что
и , что
и 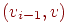 ,
и ,
и 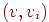 являются дугами в являются дугами в  . При этом требуемым
орциклом является (рис. 9.7) . При этом требуемым
орциклом является (рис. 9.7) 
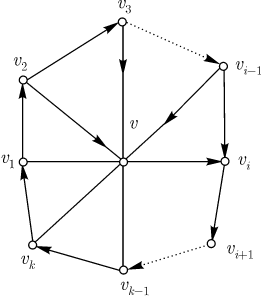
Рис. 9.7.
Если не существует вершин, обладающих указанным выше свойством, то
множество вершин, не содержащихся в орцикле, можно разбить на два
непересекающихся множества  и и  ,
где ,
где  есть множество
таких вершин есть множество
таких вершин  , что , что  для
любого для
любого  является дугой,
а является дугой,
а  есть множество таких вершин есть множество таких вершин  ,
что ,
что  для любого для любого  является дугой. Так как
является дугой. Так как  сильно связен, то оба
множества сильно связен, то оба
множества  и и  непусты, и поэтому в непусты, и поэтому в  найдется дуга
вида найдется дуга
вида  ,
где ,
где  принадлежит принадлежит  , а , а  принадлежит
принадлежит  . Тогда требуемым орциклом будет (рис. 9.8) . Тогда требуемым орциклом будет (рис. 9.8)  . .
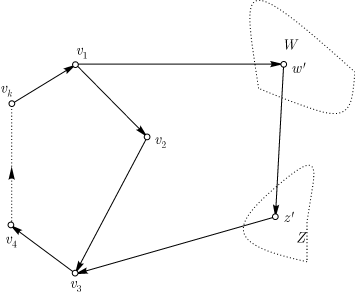
Рис. 9.8.
|








