Хроматическое числоРассмотрим задачу: при каких условиях вершины графа можно раскрасить так,
чтобы каждое ребро было инцидентно вершинам разного цвета? Нас больше
всего интересует вопрос, какие графы можно раскрасить с соблюдением
определенных условий, чем вопрос, сколькими способами можно выполнить это
раскрашивание. Пусть граф  не имеет петель; тогда не имеет петель; тогда  называется
называется  -
раскрашиваемым, если каждой его вершине можно приписать один
из -
раскрашиваемым, если каждой его вершине можно приписать один
из  цветов таким образом, чтобы никакие две смежные вершины не оказались
одного цвета. Если граф цветов таким образом, чтобы никакие две смежные вершины не оказались
одного цвета. Если граф  является является
 -раскрашиваемым, но не является -раскрашиваемым, но не является
 -раскрашиваемым, назовем его -раскрашиваемым, назовем его  -хроматическим, а
число -хроматическим, а
число  назовем хроматическим числом графа назовем хроматическим числом графа  и обозначим через
и обозначим через 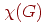 . На рисунке изображен 4-хроматический (и, следовательно, . На рисунке изображен 4-хроматический (и, следовательно,
 -раскрашиваемый граф при -раскрашиваемый граф при  ) граф; цвета
обозначены греческими
буквами. ) граф; цвета
обозначены греческими
буквами. 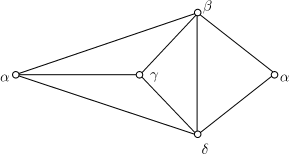
Для удобства будем предполагать, что все графы не содержат петель. Однако
будем допускать существование кратных ребер, так как они не влияют на наши
рассуждения. Ясно, что 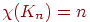 , и, следовательно, легко построить
графы со сколь угодно большим хроматическим числом. С другой стороны, нетрудно
видеть, что , и, следовательно, легко построить
графы со сколь угодно большим хроматическим числом. С другой стороны, нетрудно
видеть, что 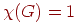
тогда и только тогда, если  — вполне несвязный граф, и что — вполне несвязный граф, и что 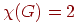
тогда и только тогда, если  — двудольный граф, отличный от
вполне несвязного графа. — двудольный граф, отличный от
вполне несвязного графа. Теорема 8.1.
Если наибольшая из степеней вершин графа  равна равна
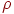 , то этот
граф , то этот
граф  -раскрашиваем. -раскрашиваем. Доказательство Проведем индукцию по числу вершин в  .
Пусть .
Пусть  — граф с — граф с  вершинами; если из него удалить произвольную вершину
вершинами; если из него удалить произвольную вершину  вместе с
инцидентными ей ребрами, то в оставшемся графе будет вместе с
инцидентными ей ребрами, то в оставшемся графе будет  вершин,
причем степени вершин по-прежнему не превосходят вершин,
причем степени вершин по-прежнему не превосходят 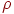 . По предположению
индукции этот граф . По предположению
индукции этот граф  -раскрашиваем, отсюда получится -раскрашиваем, отсюда получится
 -раскладка для -раскладка для  , если окрасить вершину , если окрасить вершину  цветом, отличным от тех, которыми окрашены смежные с ней вершины, а их не более
чем
цветом, отличным от тех, которыми окрашены смежные с ней вершины, а их не более
чем 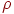 . . Теорема (Брукса).
Пусть  — простой связный граф, не являющийся полным; если
наибольшая
из степеней его вершин равна — простой связный граф, не являющийся полным; если
наибольшая
из степеней его вершин равна 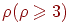 , то он , то он
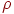 -раскрашиваем. -раскрашиваем.
Доказательство Проведем индукцию по числу вершин графа  . Предположим,
что . Предположим,
что  имеет имеет  вершин. Если при этом степень какой-нибудь его вершины
меньше вершин. Если при этом степень какой-нибудь его вершины
меньше 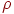 , дальше можно рассуждать, как в доказательстве
теоремы 1, и все будет закончено. Поэтому без потери общности можно считать
граф , дальше можно рассуждать, как в доказательстве
теоремы 1, и все будет закончено. Поэтому без потери общности можно считать
граф  регулярным степени регулярным степени 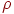 . . Выберем произвольную вершину  и удалим ее, вместе с
инцидентными ей ребрами. Останется граф с и удалим ее, вместе с
инцидентными ей ребрами. Останется граф с  вершинами, в котором наибольшая из
степеней вершин не превосходит вершинами, в котором наибольшая из
степеней вершин не превосходит 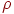 . По предположению индукции
этот граф . По предположению индукции
этот граф 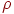 -раскрашиваем. Теперь окрасим вершину -раскрашиваем. Теперь окрасим вершину  в
один из имеющихся в
один из имеющихся 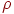 цветов. Как и раньше, считаем, что смежные с цветов. Как и раньше, считаем, что смежные с  вершины
вершины  расположены вокруг расположены вокруг  по часовой стрелке и
окрашены в различные цвета по часовой стрелке и
окрашены в различные цвета 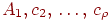 . . Определяя подграфы 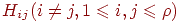 , когда , когда
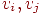 лежат в разных компонентах графа лежат в разных компонентах графа  . Таким образом, можно считать, что при любых данных
. Таким образом, можно считать, что при любых данных  вершины вершины
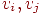 связаны простой цепью, целиком лежащей в связаны простой цепью, целиком лежащей в  . Обозначим компоненту
графа . Обозначим компоненту
графа  , содержащую вершины , содержащую вершины 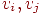 , через , через
 . . Ясно, что если вершина  — смежная более чем с одной
вершиной цвета — смежная более чем с одной
вершиной цвета  , то существует цвет, отличный от , то существует цвет, отличный от  ,
не приписанный никакой из вершин, смежных с ,
не приписанный никакой из вершин, смежных с  . Тогда
вершину . Тогда
вершину  можно
окрасить в этот цвет, что, в свою очередь, позволит окрасить вершину можно
окрасить в этот цвет, что, в свою очередь, позволит окрасить вершину
 в цвет в цвет  и закончить на этом доказательство теоремы. Если этот
случай не имеет места, то используем аналогичное рассуждение, чтобы
показать, что каждая вершина из и закончить на этом доказательство теоремы. Если этот
случай не имеет места, то используем аналогичное рассуждение, чтобы
показать, что каждая вершина из  (отличная
от (отличная
от  и от и от  ) должна иметь степень 2. Предположим, что ) должна иметь степень 2. Предположим, что
 — первая
вершина простой цепи из — первая
вершина простой цепи из  в в  , которая
имеет степень больше 2; тогда , которая
имеет степень больше 2; тогда  можно перекрасить в цвет, отличный
от можно перекрасить в цвет, отличный
от  или или  ,
нарушая тем самым свойство, что ,
нарушая тем самым свойство, что  и и  связаны простой цепью, целиком лежащей в
связаны простой цепью, целиком лежащей в  . Поэтому мы можем считать, что для
любых . Поэтому мы можем считать, что для
любых  и и 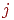 компонента компонента  состоит только из простой
цепи, соединяющей вершину состоит только из простой
цепи, соединяющей вершину  с с  . . Заметим теперь, что две простые цепи вида  и
и  , где , где  , можно считать пересекающимися только в вершине , можно считать пересекающимися только в вершине  ,
так как если ,
так как если  — другая точка пересечения, то ее можно перекрасить
в цвет, отличный от — другая точка пересечения, то ее можно перекрасить
в цвет, отличный от  или или  , или , или
 , а это противоречит
факту, что , а это противоречит
факту, что  связаны простой цепью. связаны простой цепью. Для завершения доказательства выберем (если это возможно) две несмежные
вершины 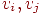 и допустим, что и допустим, что  —
вершина цвета —
вершина цвета  ,
смежная с ,
смежная с  . Поскольку . Поскольку  — простая
цепь (для любого — простая
цепь (для любого  ), можно поменять между собой цвета вершин в этой цепи, не затрагивая
раскраску остальной части графа. Но это приводит к противоречию, потому
что тогда ), можно поменять между собой цвета вершин в этой цепи, не затрагивая
раскраску остальной части графа. Но это приводит к противоречию, потому
что тогда  будет общей вершиной простых
цепей будет общей вершиной простых
цепей  и и  .
Отсюда следует, что нельзя выбрать две вершины .
Отсюда следует, что нельзя выбрать две вершины  и
и  несмежными, и поэтому несмежными, и поэтому  должен быть полным графом должен быть полным графом  . А так как это не допускается условием теоремы, то все возможные случаи
рассмотрены. . А так как это не допускается условием теоремы, то все возможные случаи
рассмотрены. Гипотеза о четырех краскахУже сто с лишним лет математики пытаются доказать гипотезу четырех красок.
В этом направлении был достигнут значительный прогресс. В печати появилось
сообщение (K.Appel, W.Haken, Every planar map is four colorable,
Bull. of Amer. Math. Soc., 82, \No\,5 (sept. 1976)), что гипотезу четырех
красок удалось обосновать с использованием ЭВМ. Сформулируем без доказательства несколько относящихся к этой проблеме
результатов. - Если гипотеза четырех красок не верна, то любой опровергающий ее пример
будет очень сложным. Известно, например, что всякий планарный граф,
имеющий менее
 вершин, 4-раскрашиваем. вершин, 4-раскрашиваем. - Любой не содержащий треугольников планарный граф 3-раскрашиваем (теорема Греча).
- Если попытаться доказать гипотезу четырех красок, то достаточно доказать
ее для гамильтоновых планарных графов (довольно неожиданный результат Уитни).
Раскрашивание картВозникновение гипотезы четырех красок исторически связано с раскрашиванием
географических карт. Если имеется карта с изображением нескольких стран,
то интересно узнать, сколько понадобится цветов для такой раскраски этих
стран, чтобы никакие две соседние страны не были окрашены в один и тот же
цвет. Возможно, самая привычная форма гипотезы четырех красок такова:
любую карту можно раскрасить с помощью четырех красок. Чтобы сделать это утверждение точным, надо определить, что означает слово
"карта". Поскольку в рассматриваемых нами задачах о раскраске
требуется, чтобы страны, расположенные по обе стороны ребра, были разного цвета,
придется исключить карты, обладающие мостом. Таким образом, удобно
определить
карту как связный плоский граф, не содержащий мостов.
Заметим, что при таком определении карты не исключаем петель или кратных ребер. Назовем карту  - раскрашиваемой, если ее грани можно
раскрасить - раскрашиваемой, если ее грани можно
раскрасить  красками так, чтобы никакие две смежные грани, то
есть грани, границы которых имеют общее ребро, не были одного цвета. Там, где
можно запутаться, будем использовать термин вершинно красками так, чтобы никакие две смежные грани, то
есть грани, границы которых имеют общее ребро, не были одного цвета. Там, где
можно запутаться, будем использовать термин вершинно  - раскрашиваемой , имея в виду - раскрашиваемой , имея в виду  -раскрашиваемость в
описанном выше смысле. Например, изображенный ниже граф является 3-раскрашиваемым
и вершинно 4-раскрашиваемым. -раскрашиваемость в
описанном выше смысле. Например, изображенный ниже граф является 3-раскрашиваемым
и вершинно 4-раскрашиваемым. 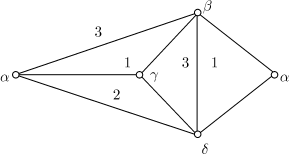
Теперь сформулируем гипотезу четырех красок для карт: всякая
карта 4-раскрашиваема. Теорема 8.3.
Карта  является 2-раскрашиваемой тогда и только
тогда, если является 2-раскрашиваемой тогда и только
тогда, если  представляет собой эйлеров граф. представляет собой эйлеров граф.
Доказательство Любую вершину  из из  должно окружать
четное число граней, так как их можно раскрасить в два цвета. Отсюда следует, что степень каждой
вершины четна, и поэтому должно окружать
четное число граней, так как их можно раскрасить в два цвета. Отсюда следует, что степень каждой
вершины четна, и поэтому  — эйлеров граф. — эйлеров граф.
Жордановой кривой, или жордановой дугой, на плоскости
называется непрерывная кривая, не имеющая самопересечений; замкнутой
жордановой кривой называется жорданова кривая, начало и конец
которой совпадают. Опишем метод, дающий нужную раскраску граней графа  . Выберем
произвольную грань . Выберем
произвольную грань  и окрасим ее в красный цвет. Проведем
жорданову кривую из точки и окрасим ее в красный цвет. Проведем
жорданову кривую из точки  грани грани  в некоторую точку любой
грани, причем так, чтобы эта кривая не проходила ни через какую вершину графа в некоторую точку любой
грани, причем так, чтобы эта кривая не проходила ни через какую вершину графа  .
Если на пути от точки .
Если на пути от точки  до точки до точки 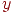 грани грани  наша кривая пересечет четное
число ребер, окрасим грань
наша кривая пересечет четное
число ребер, окрасим грань  в красный цвет; в противном
случае — в синий. в красный цвет; в противном
случае — в синий. 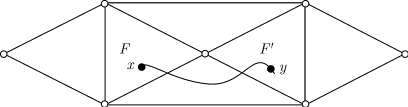
Нетрудно показать, что раскрашивание определено корректно: берем
"цикл", состоящий из двух таких жордановых кривых (то есть замкнутую жорданову
кривую), и показываем, что он пересекает четное число ребер графа
 (надо использовать индукцию по числу вершин, находящихся внутри цикла, и
тот факт, что каждой вершине графа (надо использовать индукцию по числу вершин, находящихся внутри цикла, и
тот факт, что каждой вершине графа  инцидентно четное число ребер). инцидентно четное число ребер).
|


