INTUIT.ru::Интернет-Университет Информационных Технологий

Интернет-Университет Информационных Технологий

http://www.INTUIT.ru

Графы и их применение

7. Лекция: Графы с цветными ребрами
Реберная раскраска. Задачи на графы с цветными ребрами и вытекающие из них свойства. Задача о несцепленных треугольниках с одноцветными сторонами.

Реберная раскраска

Граф называется реберно -раскрашиваемым, если его ребра можно раскрасить красками таким образом, что никакие два смежных ребра не окажутся одного цвета. Если граф реберно -раскрашиваем, но не является реберно -раскрашиваемым, то называется хроматическим классом или хроматическим индексом, или реберно-хроматическим числом графа . При этом используется запись $\chi_{e}(G)=k$ . На рисунке изображен граф , для которого $\chi_{e}(G)=4$ .

Ясно, что если наибольшая из степеней вершин графа равна $\rho$ , то $\chi_{e}(G)\ge \rho$ . Следующий результат, известный как теорема Визинга, дает точные оценки для хроматического класса графа . Доказательство этой теоремы можно найти у Оре (Ore O. The four-color problem, Academic Press, New York, 1967).

Теорема 7.1.(Визинг, 1964) Пусть в графе , не имеющем петель, наибольшая из степеней вершин равна $\rho;$ тогда $\rho \le \chi _{e} (G)\le \rho +1$ .

Задача, состоящая в выяснении того, какие графы имеют хроматический класс $\rho$ , а какие $\rho +1$ , не решена. Однако в некоторых частных случаях соответствующие результаты находятся легко. Например, $\chi_{e} (C_{n})=2$ или 3 в зависимости от того, четно или нечетно, а $\chi_{e}(W_{n} )=n-1$ , при $n\ge 4$ . Хроматические классы полных графов и полных двудольных графов вычисляются тоже просто.

Теорема 7.2. $\chi _{e} (K_{m,n} )=\rho =\max (m,n)$ .

Доказательство

Без потери общности можно считать, что $m\ge n$ и что граф $K_{m,n}$ изображен так:

вершин расположены на горизонтальной линии под вершинами. Тогда искомая реберная раскраска получается последовательным окрашиванием ребер, инцидентных этим вершинам, с использованием следующих групп красок:

$\{1,2\dts m\};\{2,3\dts m,1\};\ldots ;\{n\dts m,1\dts n-1\};$

при этом краски из каждой группы располагаются по часовой стрелке, вокруг соответствующей вершины.

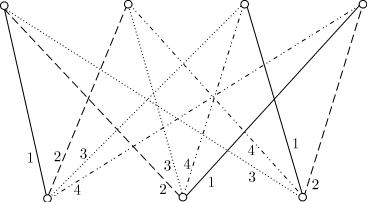
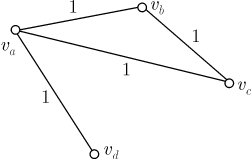
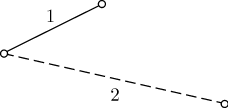
Теорема 7.3. $\chi_{e}(K_{n})=n$ , если нечетно $(n\ne 1)$ , и $\chi _{e}(K_{n})=n-1$ , если четно.

Доказательство

В случае нечетного расположим вершины графа $K_{n}$ в виде правильного -угольника. Тогда его ребра можно раскрасить следующим образом: сначала окрашиваем каждую сторону -угольника в свой цвет, а затем каждое из оставшихся ребер, диагонали -угольника, окрашиваем в тот же цвет, что и параллельная ему сторона.

То, что граф $K_{n}$ не является реберно -раскрашиваемым, сразу же следует из того, что максимально возможное число ребер одного цвета равно .

В случае четного $n(\ge 4)$ граф $K_{n}$ можно рассматривать как соединение полного — графа $K_{n-1}$ и отдельной вершины. Если в $K_{n-1}$ окрасить ребра описанным выше способом, то для каждой вершины останется один неиспользованный цвет, причем все эти неиспользованные цвета будут различными. Таким образом, чтобы получить реберную раскраску $K_{n}$ , достаточно окрасить оставшиеся ребра в соответствующие "неиспользованные" цвета.

Задачи на графы с цветными ребрами и вытекающие из них свойства

Рассматриваем графы, соответствующие таким ситуациям, в которых одни пары элементов множества находятся между собой в одном отношении, другие пары этого множества — в другом отношении, третьи — в третьем, но каждая пара — в одном отношении. Например, среди участников шахматного турнира к какому-то моменту могут быть такие, которые уже сыграли партию друг с другом, и такие, которые не сыграли. Среди множества стран есть страны, установившие между собой дипломатические связи, и страны, между которыми не установлены дипломатические связи. Для удобства на рисунках графов ребра, соответствующие одному отношению, окрашивают в один цвет, а ребра, соответствующие другому отношению, — во второй цвет, в третий цвет и т.д. Так как мы не можем выполнить рисунок в разных цветах, то присваиваем ребрам номера. Такие графы называются графами с цветными ребрами.

Свойства полных графов с цветными ребрами

Задача 1. Шесть человек участвуют в шахматном турнире, который проводится в один круг, то есть каждый шахматист встречается со всеми участниками по одному разу. Нужно доказать, что среди них всегда найдутся три участника турнира, которые провели уже все встречи между собой или еще не сыграли друг с другом ни одной партии.

Решение. Любые два участника турнира находятся между собой в одном из двух отношений: они либо уже сыграли между собой, либо еще не сыграли.

Каждому участнику поставим в соответствие вершину графа. Соединим вершины попарно ребрами двух цветов. Пусть ребро красного цвета (обозначенное цифрой 1) означает, что двое уже сыграли между собой, а синего (пронумерованное цифрой 2) — что не сыграли. Получим полный граф с шестью вершинами и ребрами двух цветов.

Теперь для решения задачи достаточно доказать, что в таком графе обязательно найдется "треугольник" с одноцветными сторонами.

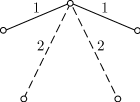
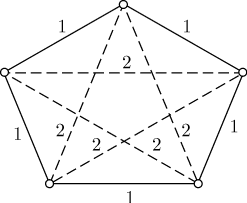
Каждая вершина полученного графа принадлежит пяти ребрам. Скольким шахматистам одного цвета может принадлежать произвольная вершина такого графа? Пять принадлежащих одной вершине ребер могут быть окрашены без учета порядка следующим образом: , , , , , . То есть каждая вершина принадлежит, по меньшей мере, трем шахматистам одного цвета. Пусть, например, вершина $v_{a}$ принадлежит трем ребрам красного цвета:

Какого цвета ребра могут соединять вершины $v_{b}$ , $v_{c}$ и $v_{d}$ ? Если хотя бы одно из них окажется красным, как на рисунке,

то получится треугольник с красными сторонами. Если же все эти ребра синие, как на рисунке,

то они вместе образуют "треугольник" с синими сторонами.

Задача решена. Рассмотрены все возможности. В каждом случае нашлись три шахматиста, или все сыгравшие между собой по одной партии, или не сыгравшие между собой ни одной партии.

Кроме того, при ее решении доказаны два свойства таких графов.

Свойство 1. Любая вершина полного графа с шестью или более вершинами и ребрами двух цветов принадлежит, по меньшей мере, трем ребрам одного цвета.

Свойство 2. В любом полном графе с шестью или более вершинами и ребрами двух цветов найдется, по меньшей мере, один треугольник с одноцветными сторонами.

Задача 2. На географической карте выбраны пять городов. Известно, что среди них из любых трех найдутся два, соединенные авиалиниями, и два — несоединенные. Требуется доказать, что:

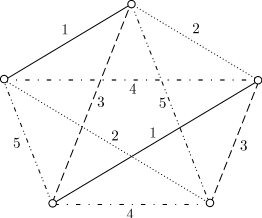
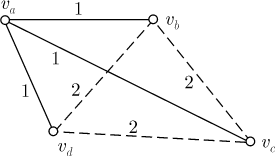
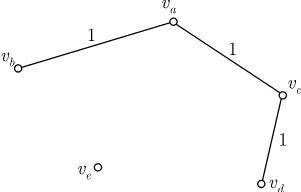
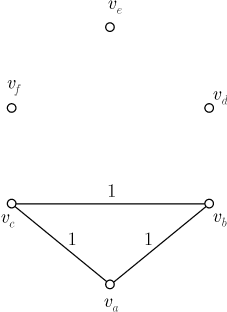
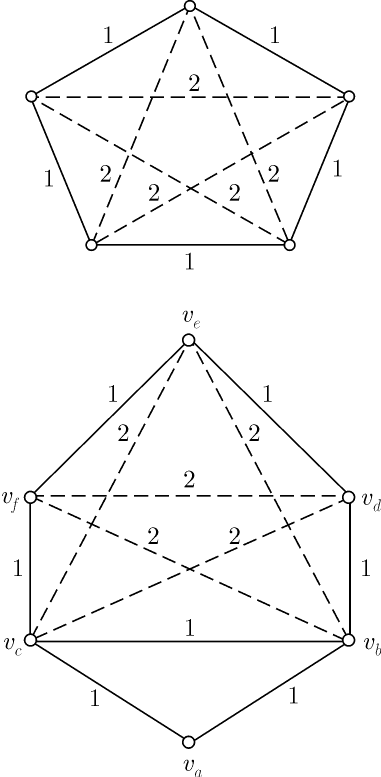
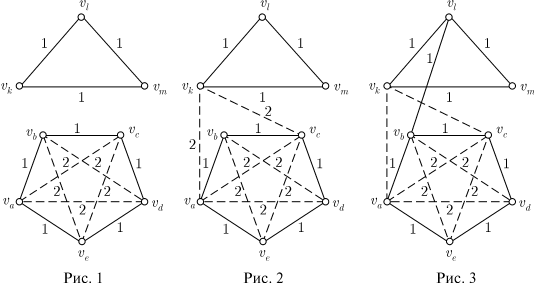
Каждый город соединен авиалиниями непосредственно с двумя и только с двумя другими городами.
Вылетев из любого города, можно облететь остальные, побывав в каждом по одному разу, и вернуться назад.

Решение. Рассматривается множество объектов — городов и два отношения, заданные для элементов этого множества. Каждые два города находятся в одном из двух отношений — они либо соединены между собой авиалиниями, либо не соединены. Пусть вершины графа соответствуют городам: красное ребро (пронумеровано 1) соответствует наличию авиалиний, синее ребро (пронумеровано 2) соответствует отсутствию авиалиний. По условию среди трех ребер, соединяющих любые три вершины, одно — красное, второе — синее,

а это означает, что в графе нет ни одного треугольника с одноцветными сторонами. Тогда из решения предыдущей задачи следует, что каждая вершина непременно принадлежит двум красным ребрам и двум синим,

поскольку в противном случае образовался бы треугольник с одноцветными сторонами. А это и означает, что каждый город соединен авиалиниями с двумя и только с двумя городами.

Остается показать, что в графе найдется "пятиугольник", все ребра которого — красные.

Выберем одну из вершин, например $v_{a}$ , а красными будут, скажем, ребра $\{v_{a},v_{b}\},\{v_{a},v_{c}\}$

Ребро $\{v_{b},v_{c}\}$ не может быть красным, следовательно, красным является одно из ребер: либо $\{v_{c},v_{d}\}$ , либо $\{v_{c},v_{e}\}$ . Пусть красное $\{v_{c},v_{d}\}$ . Если теперь соединить красным ребром вершины $v_{d}$ и $v_{b}$ , то вершина $v_{e}$ должна быть соединена красными ребрами с вершинами, которые принадлежат уже двум красным ребрам. По условию это невозможно. Остается соединить красными ребрами вершины $v_{d}$ и $v_{e}$ , $v_{b}$ и $v_{e}$ . Остальные ребра должны быть синими.

Итак, мы получили еще одно свойство.

Свойство 3. Если в полном графе с пятью вершинами и ребрами двух цветов не найдется треугольника с одноцветными сторонами, то граф можно изобразить в виде "пятиугольника" с красными сторонами и синими диагоналями.

В формулировке свойства 3 можно заменить слово "красный" на "синий" и одновременно слово "синий" на "красный", то есть речь пойдет о пятиугольнике с синими сторонами и красными диагоналями. Это понятно, поскольку для пятиугольника и только для него характерно, что его диагонали образуют также пятиугольник.

Задача 3. В течение дня двое из шести телефонных абонентов могут поговорить друг с другом по телефону, а могут и не поговорить. Докажем, что всегда можно указать две тройки абонентов, в каждой из которых все переговорили друг с другом или все не переговорили.

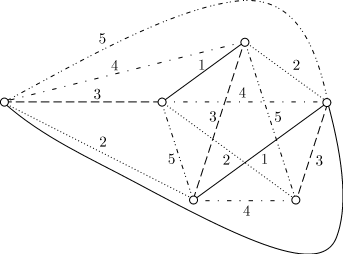
Решение. Пусть у полного графа с шестью вершинами красные ребра соответствуют парам абонентов, которые говорили друг с другом по телефону, синие — тем, кто не говорил. Тогда в графе найдется хотя бы один треугольник, $v_{a} v_{b} v_{c}$ , с одноцветными сторонами.

Остается показать, что обязательно найдется еще и второй такой треугольник.

Временно исключим из рассмотрения одну из его вершин, скажем $v_{a}$ , вместе с ребрами, принадлежащим ей.

Найдется ли в оставшемся графе с пятью вершинами треугольник с одноцветными сторонами? Если найдется, то он содержится и в исходном графе.

В противном случае получается пятиугольник с красными сторонами и синими диагоналями. Теперь восстановим шестую вершину $v_{a}$ с ее ребрами.

Если ребро $\{v_{a},v_{d}\}$ или ребро $\{v_{a},v_{f}\}$ будет окрашено в красный цвет, то образуется еще минимум один треугольник с красными сторонами $v_{a} v_{d} v_{b}$ или $v_{a} v_{c} v_{f}$ . Если оба эти ребра будут синего цвета, то появится треугольник $v_{a} v_{f} v_{d}$ с синими сторонами. Вывод нетрудно перевести с языка теории графов на язык задачи.

Установлено свойство графа, являющееся обобщением свойства 2.

Свойство 4. В любом полном графе с шестью или более вершинами и ребрами одного из двух цветов всегда найдутся два разных треугольника с одноцветными сторонами. Эти два треугольника могут иметь общую вершину или даже общее ребро.

Если два треугольника имеют общую вершину или ребро, то их называют сцепленными.

Рассмотрим свойства полного графа, ребра которого окрашены в один из трех цветов, каждый цвет соответствует одному из трех отношений между объектами заданного множества.

Задача 4. Каждый из семнадцати ученых переписывается с остальными. В их переписке речь идет лишь о трех темах. Каждая пара ученых переписывается друг с другом лишь по одной теме. Нужно доказать, что не менее трех ученых переписываются друг с другом по одной и той же теме.

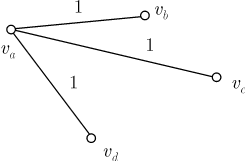
Решение. Условию задачи соответствует полный граф с семнадцатью вершинами и ребрами трех цветов. Из каждой вершины выходит шестнадцать ребер. Докажем, что в таком графе найдется хотя бы один треугольник с одноцветными сторонами. Заметим, что каждая вершина этого графа принадлежит хотя бы шести ребрам одного цвета. Пусть, например, вершина $v_{a}$ принадлежит шести красным ребрам.

Если среди вершин $v_{b}, v_{c}, v_{d}, v_{e}, v_{f}, v_{h}$ найдутся две, которые соединены красным ребром, то получится треугольник с красными сторонами. Если не найдутся, то все шесть вершин $v_{b}, v_{c}, v_{d}, v_{e}, v_{f}, v_{h}$ соединены между собой попарно ребрами двух цветов (зеленым и синим). Как было доказано ранее, в этом графе с шестью вершинами найдется хотя бы один треугольник либо с синими, либо с зелеными сторонами. Задача решена.

Сформулируем теперь свойство, доказанное при решении этой задачи.

Свойство 5. В полном графе с семнадцатью или более вершинами и ребрами трех цветов всегда найдется, по меньшей мере, один треугольник с одноцветными сторонами.

Заметим, что не случайно отношения, которые были найдены при решении задач, изображавшиеся цветными ребрами, симметричны, если $v_{a}$ — друг $v_{b}$ , то $v_{b}$ — друг $v_{a}$ , но не обязательно транзитивны, если $v_{a}$ — друг $v_{b}$ и $v_{b}$ — друг $v_{c}$ , то $v_{a}$ может и не быть другом $v_{c}$ . В случае, когда отношение между объектами было транзитивным, соответствующие ребра образовывали треугольник с одноцветными сторонами.

Задача 5. В работе международного симпозиума лингвистов участвуют человек. Из любых четырех один может объясняться с остальными тремя хотя бы на одном языке. Нужно доказать, что найдется участник симпозиума, который может объясниться с каждым из остальных участников.

Решение. Имеем полный граф с вершинами и ребрами двух цветов (синее ребро — двое могут объясниться на каком-нибудь языке, красное — не могут). По условию, среди любых четырех вершин графа всегда найдется, по меньшей мере, одна, синяя степень которой равна трем.

Случай, когда все ребра синие, тривиален, математически неинтересен. Пусть найдется красное ребро $\{v_{a},v_{b}\}$ . Добавим еще какие-нибудь две вершины $v_{c},v_{d}$ . Из четырех вершин $v_{a},v_{b},v_{c},v_{d}$ найдется хотя бы одна синяя, степень которой равна трем. Это $v_{c}$ или $v_{d}^{}$ . Пусть, например, синюю степень три имеет $v_{c}$ . Добавим еще одну вершину — $v_{e}$ . Из вершин $v_{a},v_{b},v_{c},v_{e}$ или $v_{c}$ или $v_{e}$ имеет синюю степень, равную трем. В обоих случаях $v_{c}$ соединена синим ребром с $v_{e}$ . Переберем все вершины. В итоге окажется, что $v_{c}$ соединена синим ребром со всеми вершинами графа. Во всякой четверке вершин, включая $v_{a}$ и $v_{b}$ , есть вершина, соединенная синим ребром со всеми остальными вершинами графа. Отсюда, кроме $v_{a}$ и $v_{b}$ , существует самое большее одна вершина, не соединенная синим ребром со всеми остальными.

Задача о несцепленных треугольниках с одноцветными сторонами

Задача 6. Назовем группу людей "однородной", если любая пара из этой группы психологически совместима или, напротив, любая пара психологически несовместима. Нужно доказать, что среди восьми случайно встретившихся незнакомцев всегда найдутся две однородные группы, состоящие из трех человек каждая, причем никто из первой группы не входит во вторую.

Иначе говоря, требуется доказать, что в графе с восемью вершинами и ребрами, окрашенными в один из двух цветов, обязательно найдутся два треугольника с одноцветными сторонами, не сцепленные между собой.

Решение. Рассмотрим в графе один из треугольников $v_{k} v_{l} v_{m}$ с одноцветными сторонами. По теореме 3, такой треугольник всегда найдется. Если остальные пять вершин и ребра, соединяющие их попарно, содержат еще один треугольник с одноцветными сторонами, то он и будет являться вторым искомым треугольником. (Для этого случая задача решена.) Если остальные пять вершин $v_{a},v_{b},v_{c},v_{d},v_{e}$ не содержат треугольника с одноцветными сторонами, то они образуют пятиугольник с красными сторонами и синими диагоналями. На рисунке (рис. 1) изображены не все ребра графа, соответствующего задаче, а лишь треугольник $v_{k} v_{l} v_{m}$ с красными сторонами и пятиугольник $v_{a} v_{b} v_{c} v_{d} v_{e}$ с красными сторонами и синими диагоналями.

Покажем, что если какая-нибудь вершина треугольника $v_{k} v_{l} v_{m}$ соединена синими ребрами с двумя вершинами пятиугольника, через одну, например $v_{k}$ с $v_{a}^{}$ и $v_{c}$ (рис. 2), то найдется еще один треугольник с одноцветными сторонами, не сцепленный с треугольником $v_{k} v_{a} v_{c}$ .

Действительно, обратим внимание на пятиугольник $v_{l} v_{m} v_{b} v_{d} v_{e}$ . Если он содержит треугольник с одноцветными сторонами, то второй треугольник с одноцветными сторонами, не сцепленный с первым, найден. Если не содержит, то ребра $\{v_{b}, v_{l}\},\{v_{b},v_{m}\}$ — красные, поскольку ребра $\{v_{b},v_{d}\},\{v_{b},v_{e}\}$ , по свойству 3 — уже синие. То есть образован треугольник $v_{b} v_{l} v_{m}$ с красными сторонами, не сцепленный с треугольником $v_{a} v_{c} v_{k}$ (рис. 3).

Остается рассмотреть случаи, когда каждая вершина треугольника $v_{k} v_{l} v_{m}$ соединена красными ребрами, по меньшей мере, с тремя последовательными вершинами пятиугольника $v_{a} v_{b} v_{c} v_{d} v_{e}$ . Тогда у пятиугольника найдутся две вершины, каждая из которых соединена красными ребрами с двумя вершинами треугольника $v_{k} v_{l} v_{m}$ . На (рис. 4) и (рис. 5) показаны все такие случаи. На (рис. 1.) легко обнаружить два несцепленных треугольника $v_{a} v_{b} v_{k}$ и $v_{c} v_{d} v_{m}$ . А на (рис. 5) хотя бы одно из ребер $\{ v_{a},v_{l}\}, \{v_{c},v_{l}\}$ должно быть красным (иначе вершина $v_{l}$ будет соединена синими ребрами с двумя вершинами пятиугольника $v_{a} v_{b} v_{c} v_{d} v_{e}$ , взятыми через одну, а этот случай уже рассмотрен).

Если хотя бы одно из ребер $\{v_{a},v_{l}\}$ или $\{ v_{c},v_{l}\}$ — красное, то появятся треугольники $v_{c} v_{l} v_{m}$ и $v_{a} v_{b} v_{k}$ или треугольники $v_{a} v_{k} v_{l}$ и $v_{b} v_{c} v_{m}$ с красными сторонами. Таким образом, во всех случаях найдутся два несцепленных треугольника с одноцветными сторонами. Задача решена и установлено еще одно свойство.

Свойство 6. В полном графе с восемью вершинами, ребра которого окрашены в два цвета, обязательно найдутся два треугольника с одноцветными сторонами, которые не являются сцепленными.