Бесконечные графыВ данной лекции мы обобщим некоторые определения на случай бесконечных
графов.
Бесконечным графом называется пара 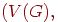
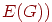 , где , где  — бесконечное множество элементов, называемое
вершинами, а — бесконечное множество элементов, называемое
вершинами, а 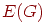 — бесконечное семейство
неупорядоченных пар элементов из — бесконечное семейство
неупорядоченных пар элементов из  , называемых ребрами. , называемых ребрами. 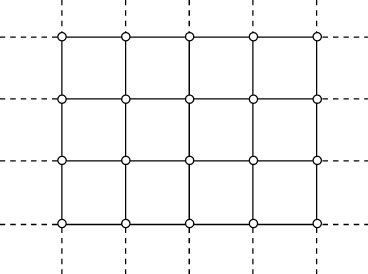
Если оба множества  и и 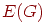 — счетны,
то — счетны,
то  называется
счетным графом. Заметим, что наши определения исключают те случаи,
когда называется
счетным графом. Заметим, что наши определения исключают те случаи,
когда  — бесконечно, а — бесконечно, а 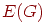 — конечно. Такие
объекты являются всего
лишь конечными графами с бесконечным множеством изолированных вершин.
Когда — конечно. Такие
объекты являются всего
лишь конечными графами с бесконечным множеством изолированных вершин.
Когда 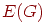 — бесконечно, а — бесконечно, а  — конечно, такие
объекты являются конечными графами с бесконечным числом петель или кратных ребер. — конечно, такие
объекты являются конечными графами с бесконечным числом петель или кратных ребер. Некоторые определения таких понятий, как "смежный",
"инцидентный",
"изоморфный", "подграф", "объединение",
"связный", "компонента"
переносятся на бесконечные графы. Степенью вершины  бесконечного графа называется мощность множества ребер,
инцидентных
бесконечного графа называется мощность множества ребер,
инцидентных  Степень вершины может быть конечной или бесконечной. Бесконечный граф, все
вершины которого имеют конечные степени, называется локально конечным. Хорошо известным примером такого графа является
бесконечная квадратная решетка, часть которой изображена на рисунке. Локально
счетный бесконечный граф — это граф, все вершины которого
имеют счетную степень. Под счетным множеством здесь и в дальнейшем понимается
бесконечное множество, допускающее взаимно однозначное отображение на
множество натуральных чисел.
Степень вершины может быть конечной или бесконечной. Бесконечный граф, все
вершины которого имеют конечные степени, называется локально конечным. Хорошо известным примером такого графа является
бесконечная квадратная решетка, часть которой изображена на рисунке. Локально
счетный бесконечный граф — это граф, все вершины которого
имеют счетную степень. Под счетным множеством здесь и в дальнейшем понимается
бесконечное множество, допускающее взаимно однозначное отображение на
множество натуральных чисел. Теорема
Каждый связный локально счетный бесконечный граф является счетным.
Доказательство Пусть  — произвольная вершина такого бесконечного
графа, и пусть — произвольная вершина такого бесконечного
графа, и пусть  — множество вершин, смежных — множество вершин, смежных  , ,
 — множество всех вершин, смежных вершинам из — множество всех вершин, смежных вершинам из  , и т.д. По условию
теоремы , и т.д. По условию
теоремы  — счетно и, следовательно,
множества — счетно и, следовательно,
множества 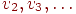 тоже счетны. Здесь используется тот
факт, что объединение не более чем счетного множества счетных множеств счетно.
Следовательно, тоже счетны. Здесь используется тот
факт, что объединение не более чем счетного множества счетных множеств счетно.
Следовательно,  —
последовательность множеств, объединение которых счетно. Кроме того, эта последовательность
содержит каждую вершину бесконечного графа в силу его связности. Отсюда и
следует нужный результат. —
последовательность множеств, объединение которых счетно. Кроме того, эта последовательность
содержит каждую вершину бесконечного графа в силу его связности. Отсюда и
следует нужный результат. Следствие
Каждый связный локально конечный бесконечный граф является счетным.
Помимо этого, на бесконечный граф  можно перенести понятие
маршрута, причем тремя различными способами: можно перенести понятие
маршрута, причем тремя различными способами: - Конечный
маршрут в
 определяется так. Маршрутом в данном
графе определяется так. Маршрутом в данном
графе  называется конечная последовательность ребер вида называется конечная последовательность ребер вида
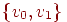 , ,  . Маршрут можно
обозначить и так: . Маршрут можно
обозначить и так:  . . - Бесконечным в одну сторону маршрутом в
 сначальной вершиной сначальной вершиной  называется бесконечная
последовательность ребер вида называется бесконечная
последовательность ребер вида 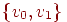 , ,  . . - Бесконечным в обе стороны маршрутом в
графе
 называется
бесконечная последовательность ребер вида называется
бесконечная последовательность ребер вида  , , 
Бесконечные в одну сторону и в обе стороны цепи и простые цепи
определяются очевидным образом, так же как и понятия длины цепи
и расстояния между вершинами. Бесконечные простые цепи не так уж трудно
обнаружить. Теорема 6.1. (Кениг, 1936)
Пусть  — связный локально бесконечный граф, тогда для любой
вершины — связный локально бесконечный граф, тогда для любой
вершины  существует бесконечная в одну сторону простая цепь с
начальной вершиной существует бесконечная в одну сторону простая цепь с
начальной вершиной  . .
Доказательство Если  — произвольная вершина графа — произвольная вершина графа  ,
отличная от ,
отличная от  , то существует нетривиальная простая цепь от , то существует нетривиальная простая цепь от  до до  ,
отсюда следует, что в ,
отсюда следует, что в  имеется бесконечно много простых цепей с начальной вершиной имеется бесконечно много простых цепей с начальной вершиной
 .
Поскольку степень .
Поскольку степень  конечна, то бесконечное множество таких
простых цепей должно начинаться с одного и того же ребра. Если таким ребром
является конечна, то бесконечное множество таких
простых цепей должно начинаться с одного и того же ребра. Если таким ребром
является 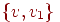 , то, повторяя эту процедуру для
вершины , то, повторяя эту процедуру для
вершины  , получим новую вершину , получим новую вершину  и соответствующее ей
ребро и соответствующее ей
ребро 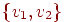 . Продолжая таким образом, получим
бесконечную в одну сторону простую цепь . Продолжая таким образом, получим
бесконечную в одну сторону простую цепь  . . Важное значение леммы Кенига состоит в том, что она позволяет получить
результаты о бесконечных графах из соответствующих результатов для
конечных графов. Типичным примером является следующая теорема. Теорема 6.2.
Пусть  — счетный граф, каждый конечный подграф которого
планарен, тогда и — счетный граф, каждый конечный подграф которого
планарен, тогда и  планарен. планарен.
Доказательство Так как  — счетный граф, его вершины можно
занумеровать в последовательность — счетный граф, его вершины можно
занумеровать в последовательность  . Исходя из нее,
построим строго возрастающую последовательность . Исходя из нее,
построим строго возрастающую последовательность 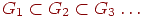 подграфов графа подграфов графа  , выбирая в
качестве , выбирая в
качестве  подграф с вершинами подграф с вершинами  и ребрами графа и ребрами графа  ,
соединяющими только эти вершины между собой. Далее, примем на веру тот факт, что
графы ,
соединяющими только эти вершины между собой. Далее, примем на веру тот факт, что
графы  могут быть уложены на плоскости конечным числом, скажем могут быть уложены на плоскости конечным числом, скажем 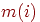 ,
топологически различных способов, и построим еще один бесконечный
граф ,
топологически различных способов, и построим еще один бесконечный
граф  . Его вершины . Его вершины  , ,  пусть соответствуют различным укладкам графов пусть соответствуют различным укладкам графов 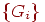 , а его ребра
соединяют те из вершин , а его ребра
соединяют те из вершин  и и  , для
которых , для
которых 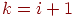 и плоская укладка, соответствующей и плоская укладка, соответствующей  . Мы видим, что
граф . Мы видим, что
граф  связен и локально конечен, поэтому, как следует из леммы Кенига, он содержит
бесконечную в одну сторону простую цепь. А так как граф связен и локально конечен, поэтому, как следует из леммы Кенига, он содержит
бесконечную в одну сторону простую цепь. А так как граф  является счетным, то эта бесконечная простая цепь и дает требуемую плоскую укладку
графа
является счетным, то эта бесконечная простая цепь и дает требуемую плоскую укладку
графа  . . Стоит подчеркнуть, что если принять дальнейшие аксиомы теории множеств,
в частности, аксиому выбора для несчетных множеств, то многие результаты
можно перенести и на такие бесконечные графы, которые необязательно
являются счетными. Краткий обзор свойств бесконечных эйлеровых графов
Связный бесконечный граф  называется эйлеровым,
если в нем существует бесконечная в обе стороны цепь, содержащая каждое ребро
графа называется эйлеровым,
если в нем существует бесконечная в обе стороны цепь, содержащая каждое ребро
графа  . Такая бесконечная цепь называется (двусторонней)
эйлеровой цепью. Назовем граф . Такая бесконечная цепь называется (двусторонней)
эйлеровой цепью. Назовем граф  полуэйлеровым,
если в нем существует бесконечная (в одну или в обе стороны) цепь, содержащая каждое
ребро графа полуэйлеровым,
если в нем существует бесконечная (в одну или в обе стороны) цепь, содержащая каждое
ребро графа  . . Теорема 6.3.
Пусть  — связный счетный граф, являющийся эйлеровым. Тогда: — связный счетный граф, являющийся эйлеровым. Тогда: - В графе
 нет вершин нечетной степени. нет вершин нечетной степени. - Для каждого конечного подграфа
 графа графа  бесконечный граф
бесконечный граф  (полученный путем удаления из
(полученный путем удаления из  ребер графа ребер графа  )
имеет не более двух бесконечных связных компонент. )
имеет не более двух бесконечных связных компонент. - Если, кроме того, степень любой вершины из
 четна,
то четна,
то  имеет ровно одну бесконечную связную компоненту. имеет ровно одну бесконечную связную компоненту.
Доказательство - Предположим, что
 — эйлерова цепь в графе — эйлерова цепь в графе
 . Тогда при всяком прохождении цепи . Тогда при всяком прохождении цепи  через любую из вершин графа степень этой
вершины увеличивается на два. А так как каждое ребро встречается в через любую из вершин графа степень этой
вершины увеличивается на два. А так как каждое ребро встречается в  ровно один раз, то каждая вершина должна иметь четную степень. Получим, что степень
любой вершины из
ровно один раз, то каждая вершина должна иметь четную степень. Получим, что степень
любой вершины из  должна быть либо четной, либо бесконечной. должна быть либо четной, либо бесконечной. - Разобьем цепь
 на три подцепи на три подцепи 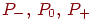 так,
что так,
что  — конечная цепь, содержащая все ребра
графа — конечная цепь, содержащая все ребра
графа  (и, быть может, другие ребра), а (и, быть может, другие ребра), а  — две бесконечные в
одну сторону цепи. Тогда бесконечный граф — две бесконечные в
одну сторону цепи. Тогда бесконечный граф  , образованный ребрами
цепей , образованный ребрами
цепей  (а также инцидентными вершинами), имеет не
более двух бесконечных компонент. Так как (а также инцидентными вершинами), имеет не
более двух бесконечных компонент. Так как  получается
из получается
из  присоединением лишь конечного множества ребер, то отсюда и следует нужный результат. присоединением лишь конечного множества ребер, то отсюда и следует нужный результат. - Пусть
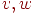 — начальная и конечная вершины
цепи — начальная и конечная вершины
цепи  . Покажем, что . Покажем, что 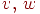 связаны в связаны в  . Если . Если  ,
то это очевидно. Если ,
то это очевидно. Если 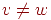 , то применяя следствие (связный графявляется
полуэйлеровымтогда и только тогда, если в нем не более двух вершин имеют нечетные степени)
к графу, полученному из , то применяя следствие (связный графявляется
полуэйлеровымтогда и только тогда, если в нем не более двух вершин имеют нечетные степени)
к графу, полученному из  путем удаления ребер
графа путем удаления ребер
графа  предполагаем , что в этом(графе ровно две
вершины, а именно предполагаем , что в этом(графе ровно две
вершины, а именно 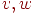 , имеют
нечетные степени), получим требуемый результат. , имеют
нечетные степени), получим требуемый результат.
Можно получить соответствующие необходимые условия для полуэйлеровых
бесконечных графов. Теорема 6.4.
Пусть  — связный счетный граф, являющийся полуэйлеровым,
но не эйлеровым. Тогда: — связный счетный граф, являющийся полуэйлеровым,
но не эйлеровым. Тогда: -
 содержит либо не более одной вершины нечетной степени, либо
не менее одной вершины бесконечной степени. содержит либо не более одной вершины нечетной степени, либо
не менее одной вершины бесконечной степени. - Для каждого конечного подграфа
 графа графа  бесконечный граф
бесконечный граф 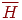 (описанный ранее) содержит ровно одну бесконечную
компоненту.
(описанный ранее) содержит ровно одну бесконечную
компоненту.
Оказывается, условие двух предыдущих теорем является не только
необходимым, но и достаточным. Этот результат сформулируем в виде
следующий теоремы, доказательство которой выходит за рамки данных лекций,
его можно найти у Оре (Оре О., Теория графов, "Наука". М.:
1968). Теорема 6.5.
Пусть  — связный счетный граф. — связный счетный граф.  является
эйлеровым графом тогда и только тогда, когда выполнены следующие условия: является
эйлеровым графом тогда и только тогда, когда выполнены следующие условия: - В графе
 нет вершин нечетной степени; нет вершин нечетной степени; - для каждого конечного подграфа
 графа графа  бесконечный граф
бесконечный граф 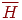 (полученный путем удаления из
(полученный путем удаления из  ребер
графа ребер
графа  ) имеет не более двух бесконечных связных компонент; ) имеет не более двух бесконечных связных компонент; - если, кроме того, степень любой вершины из
 четна,
то четна,
то 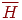 имеет ровно одну бесконечную связную компоненту. имеет ровно одну бесконечную связную компоненту.
Более того,  является полуэйлеровым тогда и только
тогда, если выполнены либо эти условия, либо следующие условия: является полуэйлеровым тогда и только
тогда, если выполнены либо эти условия, либо следующие условия: -
 содержит либо не более одной вершины нечетной степени, либо
не менее одной вершины бесконечной степени; содержит либо не более одной вершины нечетной степени, либо
не менее одной вершины бесконечной степени; - для каждого конечного подграфа
 графа графа  бесконечный граф
бесконечный граф 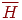 (описанный ранее) содержит ровно одну бесконечную
компоненту.
(описанный ранее) содержит ровно одну бесконечную
компоненту.
- В графе
 нет вершин нечетной степени. нет вершин нечетной степени. - Для каждого конечного подграфа
 графа
графа  бесконечный граф бесконечный граф 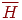 (полученный удалением из
(полученный удалением из  ребер
графа ребер
графа  ) имеет не более двух
бесконечных связных компонент. ) имеет не более двух
бесконечных связных компонент. - Если, кроме того, степень любой вершины из
 четна,
то четна,
то 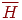 имеет ровно одну бесконечную связную компоненту. имеет ровно одну бесконечную связную компоненту.
|
