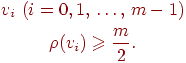INTUIT.ru::Интернет-Университет Информационных Технологий

Интернет-Университет Информационных Технологий

http://www.INTUIT.ru

Графы и их применение

5. Лекция: Гамильтоновы графы
Гамильтоновы графы. Теорема Дирака.

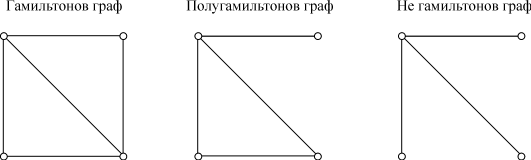
Гамильтоновы графы

Рассмотрим проблему существования замкнутой цепи, проходящей ровно один раз через каждую вершину графа .

Примеры:

Ясно, что такая цепь должна быть циклом, исключая тривиальный случай, когда является графом $N_{1}$ . Если такой цикл существует, то он называется гамильтоновым циклом (путем), а называется гамильтоновым графом. Граф, который содержит простую цепь, проходящую через каждую его вершину, называется полугамильтоновым. Название "гамильтонов цикл" возникло в связи с тем, что Уильям Гамильтон занимался исследованием существования таких циклов в графе, соответствующем додекаэдру. Додекаэдр — это многогранник, гранями которого служат 12 правильных пятиугольников. У него вершин и ребер.

Эйлеровы и гамильтоновы пути сходны по способу задания. Первые содержат все ребра, по одному разу каждое, вторые - все вершины, по одному разу каждую. Но, несмотря на внешнее сходство, задачи их поиска резко отличаются по степени трудности. Для решения вопроса о наличии эйлерова цикла в графе достаточно выяснить, все ли его вершины четны. Критерий же существования гамильтонова цикла в произвольном графе еще не найден. Решение этой проблемы имеет практическую ценность, так как к игре Гамильтона близка известная задача о коммивояжере, который должен объехать несколько пунктов и вернуться обратно. Он обязан побывать в каждом пункте в точности по одному разу и заинтересован в том, чтобы затратить на поездку как можно меньше времени. А для этого требуется определить все варианты посещения городов и подсчитать в каждом случае затрату времени. По своей математической постановке игра Гамильтона близка к задаче о порядке переналадки станков, задаче о подводке электроэнергии к рабочим местам и т.д. (Подробнее об этом рассказывается, например, в книге В.И.Мудрова "Задача о коммивояжере" М.: Знание, 1969).

Рассмотрим несколько достаточных условий существования гамильтоновых циклов в графе.

Во-первых, всякий полный граф является гамильтоновым. Действительно, он содержит такой простой цикл, которому принадлежат все вершины данного графа. Во-вторых, если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым.

Пример.

Простой (гамильтонов) цикл выделен сплошной линией , , , , . Заметим, что если граф имеет один гамильтонов цикл, то он может иметь и другие гамильтоновы циклы.

Если гамильтонов граф объединить с еще одной вершиной ребром так, что образуется висячая вершина, то такой граф гамильтоновым не является, поскольку не содержит простого цикла, проходящего через все вершины графа.

Пример.

Не является гамильтоновым и граф, представляющий собой простой цикл с "перекладиной", на которой расположены одна или несколько вершин.

Пример.

Такие графы называют "тэта графами", поскольку они похожи на греческую букву $\theta$ ("тета"). По рисунку видно, что в таком графе не удается выделить простой цикл, содержащий все вершины.

Выведем еще два достаточных признака гамильтоновых графов.

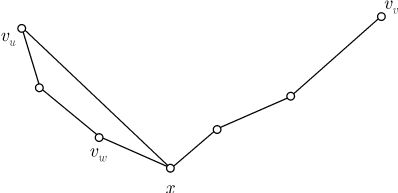
Рассмотрим граф с $m\ge3$ вершинами. Пронумеруем их произвольным образом и выпишем их последовательность:

$\eq{ v_{0},v_{1},v_{2} \dts v_{i-1}, v_{i}, v_{i+1} \dts v_{m-1}. }$ (5.1)

При этом может случиться, что некоторые две соседние вершины, например, $v_{k}$ и $v_{k+1}$ , не связаны ребром. Будем говорить, что в данной последовательности имеется "разрыв" между вершинами $v_{k}$ и $v_{k+1}$ .

Очевидно, в последовательности $v_{1},v_{2}\dts v_{i-1},v_{i}$ не возникнут другие разрывы, если ее записать в обратном порядке, а именно: $v_{i},v_{i-1} ,\ldots$ , $v_{2},v_{1}$ .

Пусть для определенности разрыв в последовательности (5.1) имеет место между вершинами $v_{0}$ и $v_{1}$ . Положим теперь, что $v_{i}$ — вершина графа , связанная ребром с $v_{0}$ . Число таких вершин $v_{i}$ равно $\rho(v_{0})$ .

Пытаясь ликвидировать разрыв в последовательности (5.1) между $v_{0}$ и $v_{1}$ , запишем ее в измененном порядке:

$\eq{ v_{0},v_{i},v_{i-1} \dts v_{2},v_{1},v_{i+1} \dts v_{m-1} }.$ (5.2)

При этом число разрывов уменьшится на единицу в том случае, если между вершинами $v_{1}$ и $v_{i+1}$ не возникнет новый разрыв.

Вершину $v_{i}$ среди вершин, не совпадающих с $v_{0}$ , можно всегда найти, так, чтобы между $v_{1}$ и $v_{i+1}$ не возник новый разрыв, если справедливо неравенство

$\rho (v_{0} ) \ge (m-1)-\rho (v_{1}) }$

(справа в этом неравенстве читаем число разрывов, которые могут произойти при всевозможных перестановках последовательности (5.1)).

Но вершины $v_{0}$ и $v_{1}$ были выбраны произвольно; можно было рассмотреть разрыв между другими соседними вершинами $v_{k}$ и $v_{k+1}$ в последовательности (5.1), можно было даже выбрать вершины $v_{u}$ и $v_{v}$ графа , не стоящие рядом в последовательности (5.1). Лишь бы соблюдалось неравенство

$\eq{ \rho (v_{u}) \ge (m-1)- \rho(v_{v}) }$ (5.3)

Заметим, что неравенство (5.3) симметрично относительно $v_{u}$ и $v_{v}$ . Его можно записать в виде

$\eq{ \rho (v_{u})+\rho(v_{v})\ge m-1. }$ (5.4)

И тогда в последовательности (5.1) удастся ликвидировать все разрывы. А это означает, что в графе найдется гамильтонов путь.

Покажем, что если для любой пары вершин $v_{u}$ и $v_{v}$ графа с вершинами справедливо неравенство

$\eq{ \rho (v_{u} )+\rho (v_{v} )\ge m, }$ (5.5)

то граф обладает гамильтоновым циклом. Это один из достаточных признаков того, что данный граф является гамильтоновым.

Рассмотрим гамильтонов путь, связывающий вершины $v_{u}$ и $v_{v}$ графа .

Пример.

Пусть — одна из вершин графа , связанная ребром с вершиной $v_{u}$ . Тогда в силу неравенства (5.5), хотя бы для одной из таких вершин найдется в гамильтоновом пути смежная с ней вершина $v_{w}$ , такая, которая связана ребром с $v_{v}$ .

Добавляя к гамильтонову пути ребра $(v_{u},x), (v_{w},v_{v})$ и выбрасывая из него ребро $(v_{w},x)$ , получаем гамильтонов цикл, что и требовалось.

Теперь, как следствие, получаем еще один достаточный признак того, что данный граф является гамильтоновым.

Формулируется этот признак так:

Граф с вершинами имеет гамильтонов цикл, если для произвольной его вершины

$\eq{ \begin{gathered} v_{i}\ (i=0,1 \dts m-1) \\ {\rho (v_{i} )\ge \frac{m}{2} }. \end{gathered} }$ (5.6)

Хотя этот признак проще, чем предыдущий (при его использовании приходится меньше считать), он позволяет распознать более узкий класс гамильтоновых графов.

Проведенное доказательство справедливости достаточных признаков гамильтоновых графов было косвенным — мы не строили для данного произвольного графа, удовлетворяющего неравенству (5.5) или неравенству (5.6), гамильтоновых циклов.

Теорема Дирака

Поиск необходимого и достаточного условия для того, чтобы граф был гамильтоновым, стал одной из главных нерешенных задач теории графов! О гамильтоновых графах, в сущности, известно очень мало. Большинство известных теорем имеет вид "если граф имеет достаточное число ребер, то граф является гамильтоновым графом". Вероятно, самой знаменитой из этих теорем является следующая теорема, принадлежащая Г.Э.Дираку и потому известная как теорема Дирака.

Теорема (Дирак, 1952) Если в простом графе с $n\ge 3$ вершинами $\rho (v)\ge n/2$ для любой вершины , то граф является гамильтоновым.

Замечание Существует несколько доказательств этой широко известной теоремы, здесь мы приводим доказательство Д.Дж.Ньюмана.

Доказательство Добавим к нашему графу новых вершин, соединяя каждую из них с каждой вершиной из . Будем предполагать, что — наименьшее число вершин, необходимых для того, чтобы полученный граф стал гамильтоновым. Затем, считая, что $k\succ 0$ , придем к противоречию.

Пусть $v\to p\to w\to \ldots \to v$ гамильтонов цикл в графе , где — вершины из , а — одна из новых вершин. Тогда не является смежной с , так как в противном случае мы могли бы не использовать вершину , что противоречит минимальности . Более того, вершина, скажем, , смежная вершине , не может непосредственно следовать за вершиной , смежной вершине , потому что тогда мы могли бы заменить $v\to p\to w\to \ldots \to v' \to w' \to \ldots \to v$ на $v\to v' \to \ldots \to w\to w' \to \ldots \to v$ , перевернув часть цикла, заключенную между и . Отсюда следует, что число вершин графа , не являющихся смежными с , не меньше числа вершин, смежных с (то есть равно, по меньшей мере, ); с другой стороны, очевидно, что число вершин графа , смежных с , тоже равно, по меньшей мере, . А так как ни одна вершина графа не может быть одновременно смежной и не смежной вершине , то общее число вершин графа , равное , не меньше, чем . Это и есть искомое противоречие.