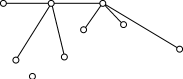
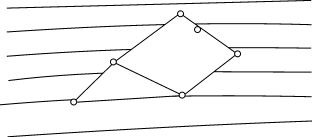
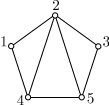
Плоский граф

Плоским графом называется граф, изображенный на плоскости так, что никакие два его ребра (или, вернее, представляющие их кривые) геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф, изоморфный плоскому графу, называется планарным. Планарный граф можно определить еще так: граф планарен, если его можно уложить на плоскости. Рисунок графа, в котором никакие два его ребра не пересекаются, если не считать точками пересечения общие вершины, называют плоским представлением графа. Ясно, что плоское представление имеет только плоский граф. Обратно, у всякого плоского графа непременно найдется плоское представление. Плоские графы — это простые циклы, деревья, лес, а также граф, содержащий цикл, из вершин которого "выходят" деревья.

Пример. Примером неплоского графа может служить полный граф с пятью вершинами. Любые попытки начертить его плоское представление обернется на неудачу.

В качестве характеристики плоского представления графа вводится понятие грани. Гранью в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.

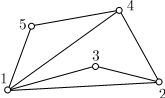
Пример. На рисунке показано плоское представление графа с тремя гранями: , , . Часть плоскости, ограниченная простым циклом , гранью не является, так как содержит цикл . Простой цикл, ограничивающий грань, называется границей грани. Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро.

Пример. В данном графе часть плоскости, ограниченная простым циклом , является гранью, так как ребро , расположенное внутри грани, не образует цикла.

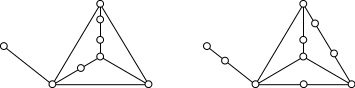
Не является гранью заштрихованная часть плоскости в данном примере, так как она содержит цикл, да к тому же эта часть плоскости не ограничена циклом. Ребро является мостом, соединяющим циклы. Такие мосты называются перегородками .

В качестве грани можно рассматривать и часть плоскости, расположенную "вне" плоского представления графа. Она ограничена "изнутри" простым циклом и не содержит других циклов. Эту часть плоскости называют бесконечной гранью.

Пример.

На рисунке часть бесконечной грани заштрихована. Всякое плоское представление графа либо не имеет бесконечной грани, либо имеет в точности одну бесконечную грань. Как особый случай вводится бесконечная грань в плоском представлении дерева и леса. В плоском представлении дерева и леса за грань принимают всю плоскость рисунка.

Два графа гомеоморфны (или тождественны с точностью до вершин степени 2), если они оба могут быть получены из одного и того же графа "включением" в его ребра новых вершин степени 2.

Пример.

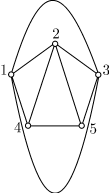
Изображенные графы гомеомофны, и то же самое можно сказать о любых двух циклических графах. Гомеоморфность графов является отношением эквивалентности. Ясно, что введение термина "гомеоморфны" удобно только с технической точки зрения — включение или удаление вершин степени 2 не имеет никакого отношения к планарности. Добавление (включение) одной вершины, скажем , в какое-нибудь ребро, например , осуществляется следующим образом: пусть ребро инцидентно вершинам и . Тогда ребро удаляется из графа, но добавляются два новых ребра: инцидентное вершинам и , и , инцидентное вершинам и .

Введение понятия гомеоморфности графов позволяет установить следующий важный результат, известный как теорема Куратовского (точнее, как теорема Понтрягина-Куратовского, так как Л.С.Понтрягин доказал, но не опубликовал, эту теорему еще в 1927 году), которая дает необходимое и достаточное условие планарности графа.

Гомеоморфные графы

Теорема (Куратовский, 1930) Граф планарен тогда и только тогда, если не содержит подграфов, гомеоморфных или .

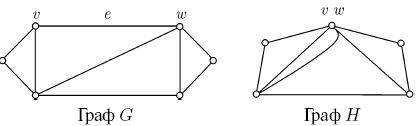
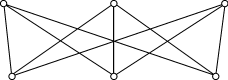
Поскольку доказательство теоремы Куратовского довольно длинное и сложное, здесь оно не приводится (см. Ф.Харари. Теория графов. М.: "Мир". 1973). Тем не менее, воспользуемся теоремой Куратовского для получения другого критерия планарности. Рассмотрим еще два определения. Элементарным стягиванием называется такая процедура: берем ребро (вместе с инцидентными ему вершинами, например, и ) и"стягиваем" его, то есть удаляем и отождествляем и . Полученная при этом вершина инцидентна тем ребрам (отличным от ), которым первоначально были инцидентны или .

Пример.

Граф называется стягиваемым к графу , если можно получить из с помощью некоторой последовательности элементарных стягиваний.

Граф планарен тогда и только тогда, если он не содержит подграфов, стягиваемых в или к .

Формула Эйлера

Для всякого плоского представления связного плоского графа без перегородок число вершин ( ), число ребер ( ) и число граней с учетом бесконечной ( ) связаны соотношением .

Пусть граф — связный, плоский граф без перегородок. Определим значение алгебраической суммы для его произвольного плоского представления.

Преобразуем данный граф в дерево, содержащее все его вершины. Для этого удалим некоторые ребра графа , разрывая поочередно все его простые циклы, причем так, чтобы граф оставался связным и без перегородок.

Заметим, что при таком удалении одного ребра число граней уменьшается на , так как при этом либо пропадет один простой цикл, либо два простых цикла преобразуются в один. Следовательно, значение разности при этом остается неизменным.

На рисунке ребра, которые мы удаляем, изображены кривыми. В полученном дереве обозначим число вершин — , число ребер — , число граней — . Справедливо равенство .

В дереве одна грань, то есть . Операция удаления ребер из графа не меняет число его вершин, то есть . По теореме 2.1 (см. лекцию 2), в дереве . Отсюда , то есть , а потому или .

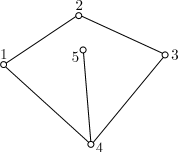
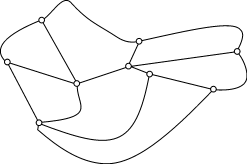
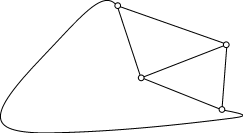
Итак, доказано, что если в плоском представлении связного графа без перегородок вершин, ребер и граней, то . Полученная формула называется формулой Эйлера.

Пример.

Триангулированный граф

Рассмотрим плоский граф с пятью вершинами.

Если добавить к нему ребра и , то полученный новый граф тоже будет плоским.

К этому графу не удается добавить ни одного ребра так, чтобы новый граф тоже был плоским.

Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским. Изображенный граф является максимально плоским.

Каждая грань в плоском представлении максимально плоского графа имеет вершины. Поэтому максимально плоский граф называют триангулированным .

Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа.

Задачи

Задача 1. На участке три дома и три колодца. От каждого дома к каждому колодцу ведет тропинка.

Когда владельцы домов поссорились, они задумали проложить дороги от каждого дома к каждому колодцу так, чтобы не встречаться на пути к колодцам. Нужно показать, что их намерения не могут осуществиться.

Решение. Для решения задачи достаточно доказать, что граф , изображенный на рисунке, не плоский.

Предположим, что граф — плоский, то есть существует его плоское представление. Граф — связный, он не имеет ни одного моста, поэтому не имеет и перегородок. По формуле Эйлера, . Здесь — число вершин, — число ребер, — число граней с учетом бесконечной грани. Подсчитаем число вершин и ребер: = 6, = 9, поэтому .

Теперь оценим удвоенное число ребер . Заметим, что в графе нет простых циклов длиной 3, то есть граница любой грани в плоском представлении графа содержит не менее четырех ребер. Заметим, что каждое ребро служит границей двух граней, так как мы учитываем и бесконечную грань. При этом число не может быть больше удвоенного числа всех ребер: . Если бы мы знали число ребер в границе каждой грани, то их сумма должна быть равна ; но известно, что , а , откуда . Полученное противоречие доказывает, что предположение было неверное, то есть граф — не плоский. Таким образом, намерения соседей неосуществимы.

Задача 2. Каждый из четырех соседей соединил свой дом с тремя другими дорожками, которые пересекались лишь около домов.

Требуется доказать, что дом пятого соседа со всеми остальными домами соединить непересекающимися дорожками невозможно, то есть он вынужден построить мост или рыть подземный ход.

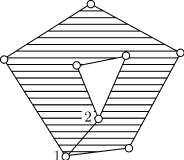
Решение. Решение задачи сводится к доказательству того, что полный граф с пятью вершинами не является плоским.

Предположим, что граф плоский, то есть существует его плоское представление. Граф — связный, он не имеет перегородок, так как не имеет ни одного моста. Для плоского представления графа верна формула Эйлера. Подсчитаем число вершин и ребер: , , тогда .

Оценим удвоенное число ребер . Каждая грань ограничена не более чем тремя ребрами (граф полный). Каждое ребро принадлежит границам двух граней, поэтому число не может быть больше числа , то есть . Но , а , то есть , . Противоречие доказывает, что предположение было неверным, то есть граф — не плоский.