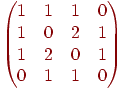Определения и примеры
Матрицей смежности графа  с множеством
вершин с множеством
вершин 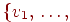  (соответствующей данной
нумерации вершин) называется матрица (соответствующей данной
нумерации вершин) называется матрица 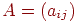 размера размера  , в которой элемент , в которой элемент  равен числу ребер в равен числу ребер в  ,
соединяющих ,
соединяющих  и и  .
Можно получить несколько различных матриц смежности данного графа, меняя
обозначения его вершин. Это приведет к изменению порядка строк и столбцов
матрицы .
Можно получить несколько различных матриц смежности данного графа, меняя
обозначения его вершин. Это приведет к изменению порядка строк и столбцов
матрицы 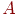 . Но в результате всегда получится симметричная матрица
из неотрицательных целых чисел, обладающая тем свойством, что сумма чисел
в любой строке или столбце равна степени соответствующей вершины. Каждая
петля учитывается в степени вершины один раз. Обратно, по любой заданной
симметричной матрице из неотрицательных целых чисел легко построить граф,
единственный с точностью до изоморфизма, для которого данная матрица
является матрицей смежности. Отсюда следует, что теорию графов можно
свести к изучению матриц особого типа. . Но в результате всегда получится симметричная матрица
из неотрицательных целых чисел, обладающая тем свойством, что сумма чисел
в любой строке или столбце равна степени соответствующей вершины. Каждая
петля учитывается в степени вершины один раз. Обратно, по любой заданной
симметричной матрице из неотрицательных целых чисел легко построить граф,
единственный с точностью до изоморфизма, для которого данная матрица
является матрицей смежности. Отсюда следует, что теорию графов можно
свести к изучению матриц особого типа. Матрицей инциденций простого графа с множеством вершин
 , ,
 называется матрица называется матрица 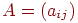 размера размера
 , у которой , у которой
 , если вершина , если вершина  инцидентна ребру инцидентна ребру
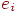 ,
и ,
и  , в противном случае. , в противном случае. Граф, у которого множество ребер пусто, называется вполне
несвязным или пустым графом. Будем обозначать вполне
несвязный граф с  вершинами через вершинами через  . Простой
граф, в котором любые две вершины смежны, называется полным графом.
Полный граф с . Простой
граф, в котором любые две вершины смежны, называется полным графом.
Полный граф с  вершинами обычно обозначается
через вершинами обычно обозначается
через  . Граф, у которого все вершины имеют одну и ту же степень, называется
регулярным графом. Если степень каждой вершины равна . Граф, у которого все вершины имеют одну и ту же степень, называется
регулярным графом. Если степень каждой вершины равна  ,
то граф называется регулярным степени ,
то граф называется регулярным степени  .
Регулярные графы степени 3 называются также кубическими,
или трехвалентными графами. Каждый вполне
несвязный граф является регулярным степени .
Регулярные графы степени 3 называются также кубическими,
или трехвалентными графами. Каждый вполне
несвязный граф является регулярным степени  ,
а каждый полный граф ,
а каждый полный граф  — регулярным
степени — регулярным
степени  . Среди
регулярных графов особенно интересны платоновы графы —
графы, образованные вершинами и ребрами пяти правильных многогранников —
платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра. . Среди
регулярных графов особенно интересны платоновы графы —
графы, образованные вершинами и ребрами пяти правильных многогранников —
платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра. Объединение и соединение двух графов. Существует несколько
способов соединения двух графов для образования нового, большего графа.
Рассмотрим два из них. Пусть даны
два графа  , ,  ,
причем множества ,
причем множества 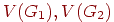 не пересекаются.
Тогда
объединением не пересекаются.
Тогда
объединением  графов
графов 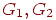 называется граф с множеством
вершин называется граф с множеством
вершин  и семейством
ребер и семейством
ребер  Можно также
образовать соединение
графов Можно также
образовать соединение
графов  , обозначаемое , обозначаемое  , взяв их
объединение и соединив ребрами каждую вершину
графа , взяв их
объединение и соединив ребрами каждую вершину
графа  с каждой вершиной
графа с каждой вершиной
графа  . . Пример матрицы
смежности. Пусть дан граф 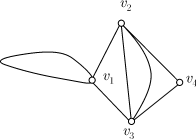
Матрица смежности 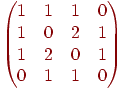
Обхватом графа называется длина его кратчайшего цикла.
Множество  ребер графа называется независимым, если оно не содержит циклов,
то есть никакая совокупность ребер из ребер графа называется независимым, если оно не содержит циклов,
то есть никакая совокупность ребер из  не образует цикла. Диаметром не образует цикла. Диаметром 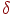 связного графа
связного графа  называется максимальное возможное
расстояние между любыми двумя его вершинами. Центром графа называется максимальное возможное
расстояние между любыми двумя его вершинами. Центром графа  называется такая вершина
называется такая вершина  , что максимальное расстояние
между , что максимальное расстояние
между  и любой другой вершиной является наименьшим из всех возможных. Это
расстояние называется радиусом и любой другой вершиной является наименьшим из всех возможных. Это
расстояние называется радиусом  . Таким образом, . Таким образом, 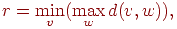
где  — расстояние между — расстояние между  и
и  . . Удаление ребер, мостыПри удалении ребра 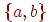 из графа из графа  получается граф с теми же
вершинами, что и граф
получается граф с теми же
вершинами, что и граф  , и всеми ребрами, кроме ребра , и всеми ребрами, кроме ребра 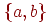 .
При удалении ребра из связного графа новый граф может оказаться как
связным, так и несвязным. Ребро .
При удалении ребра из связного графа новый граф может оказаться как
связным, так и несвязным. Ребро 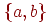 называется мостом
графа называется мостом
графа  , если в графе, полученном после удаления из , если в графе, полученном после удаления из
 ребра ребра 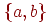 , вершины , вершины  и и  оказываются
несвязными. Существует несколько признаков мостов. Известно, что признак какого-то объекта может
заменить его определение, то есть по признаку можно распознать объект.
Рассмотрим признаки мостов. оказываются
несвязными. Существует несколько признаков мостов. Известно, что признак какого-то объекта может
заменить его определение, то есть по признаку можно распознать объект.
Рассмотрим признаки мостов. - Ребро
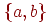 является мостом в том и только в том
случае, если является мостом в том и только в том
случае, если
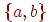 — единственный путь, соединяющий вершины — единственный путь, соединяющий вершины
 и и  . . - Ребро
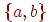 является мостом в том и только в том случае,
если найдутся две вершины является мостом в том и только в том случае,
если найдутся две вершины  и и  , такие, что каждый путь,
соединяющий их, содержит , такие, что каждый путь,
соединяющий их, содержит  и и  . . - Ребро
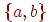 является мостом в том и только в том случае,
если оно не принадлежит ни одному циклу. является мостом в том и только в том случае,
если оно не принадлежит ни одному циклу.
Докажем справедливость третьего признака.
Прямая теорема. Если ребро 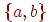 не принадлежит ни одному
циклу, то не принадлежит ни одному
циклу, то 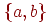 — мост. — мост.
Так как ребро 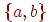 не принадлежит ни одному циклу, при его
удалении не останется пути, связывающего не принадлежит ни одному циклу, при его
удалении не останется пути, связывающего  и и  , то
есть , то
есть 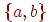 является мостом. является мостом.
Обратная теорема.
Если ребро 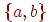 — мост, то — мост, то 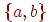 не принадлежит ни одному циклу.
не принадлежит ни одному циклу. Если бы ребро 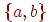 принадлежало циклу, то при удалении
ребра принадлежало циклу, то при удалении
ребра 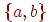 остался бы второй путь, связывающий остался бы второй путь, связывающий  и
и  ,
то есть ребро ,
то есть ребро 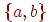 не было бы мостом.
Следовательно, не было бы мостом.
Следовательно, 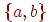 не принадлежит циклу. не принадлежит циклу. ДеревьяСвязные графы, в которых существует одна и только одна цепь, соединяющая
каждую пару вершин, называются деревьями. Дерево можно
определить и как связный граф, не содержащий циклов.
Пример.
Кубок по настольному теннису разыгрывается по олимпийской системе. Встречи
проводятся без "ничьих". К очередному туру допускается только
победившая в
предыдущем туре команда. Проигравшие команды выбывают из игры. Для
завоевания кубка команда должна победить во всех турах. На участие
в розыгрыше кубка поданы заявки от  команд. команд. Схема проведения игр изображается графом 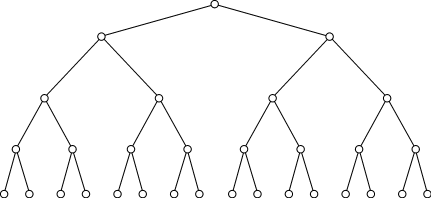
Вершины нижнего "яруса" дерева интерпретируем как команды,
участвующие в розыгрыше кубка, вершины второго снизу яруса — как команды-победительницы
в  финала, вершины третьего яруса — как
команды-победительницы
в финала, вершины третьего яруса — как
команды-победительницы
в 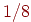 финала и т.д. финала и т.д. Какую информацию можно получить с помощью этого дерева? Непосредственно с него считываются: - Число всех участников розыгрыша кубка (число вершин нижнего
"яруса").
- Число этапов проведения розыгрыша (число "ярусов" из вершин
в дереве, не считая нижнего).
- Число команд, участвующих в
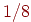 финала, в финала, в 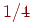 финала, в
финала, в 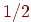 финала (число вершин, соответственно, в четвертом
сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе). финала (число вершин, соответственно, в четвертом
сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе). - Число матчей, которые придется сыграть командам для
выявления обладателя кубка (число вершин в графе без нижнего
"яруса"). Хотя это число легко определяется и без
дерева. (В каждом матче выбывает одна команда. Для того чтобы
была выявлена команда-победительница, остальные должны выбыть
из соревнования. Поэтому число матчей равно числу команд
без одной, а именно
 ). ).
Удобно считать, что граф, состоящий из одной изолированной вершины, тоже
является деревом. Для каждой пары вершин дерева существует единственный
соединяющий их путь.
Лесом называется несвязный граф,
представляющий объединение деревьев. Всякое ребро в дереве и в лесе
является мостом (признак 3). Пример. Изображен лес, состоящий из четырех компонент, каждая
из которых является деревом. 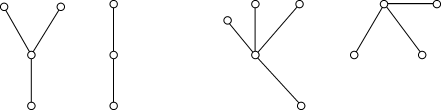
Заметим, что по определению деревья и леса являются простыми графами. По
многим показателям дерево представляет собой простейший нетривиальный тип
графа. Известно, что в связном графе  удаление одного ребра,
принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа.
Применим эту процедуру к одному из оставшихся циклов, и так до тех пор,
пока не останется ни одного цикла. В результате получим дерево,
связывающее все вершины графа удаление одного ребра,
принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа.
Применим эту процедуру к одному из оставшихся циклов, и так до тех пор,
пока не останется ни одного цикла. В результате получим дерево,
связывающее все вершины графа  , оно называется остовным
деревом или
остовом , или каркасом графа , оно называется остовным
деревом или
остовом , или каркасом графа  . . В общем случае обозначим через  произвольный граф
с произвольный граф
с  вершинами, вершинами,
 ребрами и ребрами и  компонентами. Применяя описанную выше
процедуру к каждой компоненте компонентами. Применяя описанную выше
процедуру к каждой компоненте  , получим в результате граф, называемый
остовным лесом. Число удаленных в этой процедуре ребер называется
циклическим рангом или циклическим числом
графа , получим в результате граф, называемый
остовным лесом. Число удаленных в этой процедуре ребер называется
циклическим рангом или циклическим числом
графа  и
обозначается через и
обозначается через 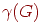 . Мы видим, что . Мы видим, что  и является неотрицательным целым числом. Таким образом, циклический ранг
дает меру связности графа: циклический ранг дерева равен нулю, а
циклический ранг циклического графа равен единице. Удобно также определить
коциклический ранг или ранг разреза графа
и является неотрицательным целым числом. Таким образом, циклический ранг
дает меру связности графа: циклический ранг дерева равен нулю, а
циклический ранг циклического графа равен единице. Удобно также определить
коциклический ранг или ранг разреза графа  как число ребер в его
остовном лесе. Коциклический ранг обозначается через как число ребер в его
остовном лесе. Коциклический ранг обозначается через 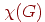 и
равен и
равен  . . Теорема 2.1
Дерево с  вершинами имеет вершинами имеет  ребро. ребро.
Доказательство Для того чтобы из одного дерева  , не являющегося
изолированной вершиной, получить два дерева с теми же вершинами, необходимо удалить из , не являющегося
изолированной вершиной, получить два дерева с теми же вершинами, необходимо удалить из
 одно ребро. Для образования трех деревьев необходимо удалить
из одно ребро. Для образования трех деревьев необходимо удалить
из  два каких-нибудь ребра. Самое большее, из дерева два каких-нибудь ребра. Самое большее, из дерева  с
с  вершинами можно получить вершинами можно получить  деревьев, каждое из которых является
изолированной вершиной. Для этого необходимо удалить деревьев, каждое из которых является
изолированной вершиной. Для этого необходимо удалить  ребро из дерева ребро из дерева
 . Итак, действительно, в дереве с . Итак, действительно, в дереве с  вершинами — вершинами —  ребро.
ребро. Перечисление деревьевТеория перечисления графов занимается разработкой методов подсчета числа
неизоморфных графов, обладающих тем или иным свойством. Вероятнее всего,
эта теория возникла в 70-х годах девятнадцатого столетия и связана с
именем Кэли, который пытался найти число насыщенных углеводородов
 , содержащих данное число атомов углерода.
Как он обнаружил,
эта задача сводится к подсчету числа деревьев, у которых степень каждой
вершины равна либо четырем, либо единице. Сейчас многие задачи по
перечислению графов решены. , содержащих данное число атомов углерода.
Как он обнаружил,
эта задача сводится к подсчету числа деревьев, у которых степень каждой
вершины равна либо четырем, либо единице. Сейчас многие задачи по
перечислению графов решены. Рассмотрим несколько определений
Помеченный граф с  вершинами — это граф, у
которого все вершины "помечены" целыми числами от 1 до вершинами — это граф, у
которого все вершины "помечены" целыми числами от 1 до  . Более
точно, определим
распределение меток в графе . Более
точно, определим
распределение меток в графе  с с  вершинами как взаимно однозначное соответствие между множеством вершин
вершинами как взаимно однозначное соответствие между множеством вершин  и
множеством и
множеством  ; тогда помеченным графом называется
пара ; тогда помеченным графом называется
пара 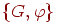 , где , где  — граф, а — граф, а
 — распределение меток
в — распределение меток
в  . Числа . Числа  будем называть метками графа будем называть метками графа  и обозначать вершины
и обозначать вершины  через через  .
Назовем два помеченных графа .
Назовем два помеченных графа 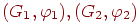 изоморфными, если существует изоморфизм между
изоморфными, если существует изоморфизм между  и
и  , сохраняющий распределение меток в этих графах. , сохраняющий распределение меток в этих графах. Пример.
Различные распределения меток в дереве с четырьмя вершинами: 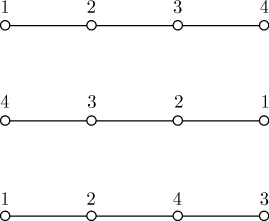
Внимательное изучение рисунка позволяет заметить, что второе помеченное
дерево является просто перевернутым первым, а отсюда следует, что эти два
помеченных дерева изоморфны. С другой стороны, ни одно из них не изоморфно
третьему помеченному дереву — достаточно посмотреть на степень
вершины  . Следовательно, общее число различных распределений
меток в данном дереве должно равняться . Следовательно, общее число различных распределений
меток в данном дереве должно равняться  , поскольку
"переворот" любого распределения меток не приводит к новому объекту. Аналогично, общее
число различных распределений меток в дереве, изображенном на рисунке,
должно равняться четырем, так как его центральная вершина может быть
помечена четырьмя различными способами, каждый из которых однозначно
определяет распределение меток. Отсюда следует, что число всех
(неизоморфных) помеченных деревьев с четырьмя вершинами равно шестнадцати.
Рассмотрим теорему Кэли, обобщающую этот результат на помеченные деревья
с , поскольку
"переворот" любого распределения меток не приводит к новому объекту. Аналогично, общее
число различных распределений меток в дереве, изображенном на рисунке,
должно равняться четырем, так как его центральная вершина может быть
помечена четырьмя различными способами, каждый из которых однозначно
определяет распределение меток. Отсюда следует, что число всех
(неизоморфных) помеченных деревьев с четырьмя вершинами равно шестнадцати.
Рассмотрим теорему Кэли, обобщающую этот результат на помеченные деревья
с  вершинами. вершинами. Теорема2.2(Кэли, 1889)
Существует ровно  различных помеченных деревьев
с различных помеченных деревьев
с  вершинами. вершинами.
Доказательство теоремы: Moon J.W. Counting labeled trees,
Canadi\-an Math. Congress, Montreal, 1970.
|