INTUIT.ru::Интернет-Университет Информационных Технологий

Интернет-Университет Информационных Технологий

http://www.INTUIT.ru

Графы и их применение

16. Лекция: Теория трансверсалей
Теория трансверсалей. Приложение теории трансверсалей.

Теория трансверсалей

Приводятся определения трансверсали. Используя эти понятия, дается еще одно доказательство теоремы Холла. Описывается несколько приложений в лексике трансверсалей.

Если — непустое конечное множество и $\varphi =(S_{1}\dts S_{m})$ — семейство (не обязательно различных) непустых его подмножеств, трансверсалью (или системой различных представлений) для $\varphi$ называется подмножество множества , состоящее из элементов: по одному из каждого множества $S_{i}$ .

Общие трансверсали. Если — непустое конечное множество, а $\varphi =(S_{1} \dts S_{m})$ и $\tau =(T_{1}\dts T_{m})$ — два семейства его непустых подмножеств, то интересно знать, когда существует общая трансверсаль для $\varphi$ и $\tau$ , то есть множество, состоящее из различных элементов множества и являющееся трансверсалью и для $\varphi$ , и для $\tau$ .

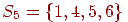Рассмотрим пример. Предположим, что $E=\{ 1,2,3,4,5,6\}$ , а $S_{1} =S_{2} =\{ 1,2\}$ , $S_{3} =S_{4} =\{ 2,3\}$ , $S_{5} =\{ 1,4,5,6\}$ . Подсемейство $\varphi' =(S_{1},S_{2},S_{3},S_{5})$ имеет трансверсаль, например $\{ 1,2,3,4\}$ . Трансверсаль произвольного подсемейства семейства $\varphi$ будем называть частичной трансверсалью для $\varphi$ ; в нашем примере семейство $\varphi$ имеет несколько частичных трансверсалей (например, $\{1,2,3,6\}$ , $\{2,3,6\}$ , $\{1,5\}$ , $\emptyset$ и т.д.). Ясно, что любое подмножество частичной трансверсали само является частичной трансверсалью.

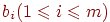Естественно спросить: при каких условиях данное семейство подмножеств некоторого множества имеет трансверсаль? Легко увидеть связь между этой задачей и задачей о свадьбах, если взять за Е множество девушек, а за $S_{i}$ — множество девушек, знакомых юноше $b_{i} (1\le i\le m)$ ; трансверсалью в этом случае является множество из девушек, такое, что каждому юноше соответствует ровно одна (знакомая ему) девушка. Следовательно, теорема Холла дает необходимое и достаточное условие существования трансверсали для данного семейства множеств. Сформулируем теорему Холла для этого случая и дадим другое ее доказательство, принадлежащее Р.Радо.

Теорема Пусть — непустое конечное множество и $\varphi =(S_{1} \dts S_{m})$ — семейство непустых его подмножеств; тогда $\varphi$ имеет трансверсаль в том и только в том случае, если для любых подмножеств $S_{i}$ их объединение содержит, по меньшей мере, элементов $(1\le k\le m)$ .

Доказательство Необходимость этого условия очевидна. Для доказательства достаточности установим, что если одно из подмножеств (скажем, $S_{1}$ ) содержит более одного элемента, то можно удалить один элемент из $S_{1}$ , не нарушив условия теоремы. Повторением этой процедуры мы добьемся сведения задачи к тому случаю, когда каждое подмножество содержит только один элемент. Тогда утверждение станет очевидным.

Осталось обосновать законность этой "процедуры сведения". Предположим, что $S_{1}$ содержит элементы и , удаление каждого из которых нарушает условие теоремы. Тогда существуют подмножества и множества $\{ 2,3\dts m\}$ , обладающие тем свойством, что

$\begin{align*} \left|\bigcup _{j\in A}S_{j} \bigcup (S_{1} -\{ x\} ) \right| & \le \left|A\right|\\ \left|\bigcup_{j\in B}S_{j} \bigcup (S_{1} -\{ y\} )\right| & \le \left|B\right|. \end{align*}$

Но эти два неравенства приводят к противоречию, поскольку

$\begin{aligned} \left|A\right|+\left|B\right|+1 & =\left|A\bigcup B \right|+\left|A\bigcap B \right|+1\le\\ & \le \left|\bigcup _{jA\bigcup B }S_{1} \bigcup S_{1} \right|+\left|\bigcup _{j\in A\bigcap B }S_{j} \right|\le \quad \t{(по условию)}\\ & \le \left|\bigcup _{j\in A}S_{j} \bigcup (S_{1} -\{ x\} ) \right|+\left|\bigcup _{j\in B}S_{j} \bigcup S_{1} -\{ y\} ) \right|\le\\ & \qquad \qquad \qquad\qquad\qquad \qquad\le \quad \t{(так как $\left|S_{1} \right|\ge 2)$}\\ & \le \left|A\right|+\left|B\right| \quad \t{(по предположению)}. \end{aligned}$

Прелесть этого доказательства в том, что оно проводится, по существу, лишь в один шаг, в отличие от доказательства Халмоша-Вогена, которое предполагает исследование двух отдельных случаев. (Однако доказательство Радо труднее перевести на весьма наглядный матримониальный язык!).

Следствие В тех же обозначениях, что и выше, $\varphi$ имеет частичную трансверсаль мощности тогда и только тогда, если для любых подмножеств $S_{i}$ их объединение содержит, по меньшей мере, элементов.

Доказательство Требуемый результат можно получить, применив теорему Холла в лексике трансверсалей к семейству $\varphi' =S_{1} \bigcup D\dts S_{m} \bigcup D$ , где — произвольное множество, не непересекающееся с и состоящее из элементов. Заметим, что $\varphi$ имеет частичную трансверсаль мощности тогда и только тогда, если $\varphi'$ имеет трансверсаль.

Следствие Если и $\varphi$ такие же, как и прежде, а — любое подмножество из , то содержит частичную трансверсаль мощности для $\varphi$ тогда и только тогда, если для каждого подмножества множества $\{1\dts m\}$

$\left|(\bigcup _{j\in A}S_{j} )\bigcap X \right|\ge \left|A\right|+t-m.$

Доказательство Достаточно применить предыдущее следствие к семейству $\varphi_{x} =(S_{1} \bigcap X\dts S_{m} \bigcup X)$ .

Приложение теории трансверсалей

Используются понятия трансверсалей, на основании чего доказывается теорема о модификации латинского прямоугольника. Вводятся определения -матрицы, формулируются и доказываются теоремы Кенига-Эгервари и об общей трансверсали.

Теорема Пусть латинский $m\times n$ -прямоугольник, причем, ; тогда можно расширить до латинского квадрата добавлением новых строк.

Доказательство Докажем, что можно расширить до латинского $(m+1)\times n$ -прямоугольника; повторяя эту процедуру, мы придем к латинскому квадрату.

Пусть $E=\{1,2\dts n\}$ и $\varphi =(S_{1}\dts S_{n})$ , где через $S_{i}$ обозначено множество, состоящее из тех элементов множества , которые не встречаются в -м столбце матрицы . Если мы сможем доказать, что $\varphi$ имеет трансверсаль, то тем самым мы докажем теорему, поскольку элементы этой трансверсали и образуют дополнительную строку. По теореме Холла достаточно доказать, что объединение любых множеств $S_{i}$ содержит по меньшей мере различных элементов. А это очевидно, ибо любое такое объединение содержит $(n-m)\times k$ элементов (включая повторения), значит, по крайней мере, один из них повторялся бы более чем раз, что невозможно.

Определение (0,1) матрицы или матрицы инциденций. Другой подход к изучению трансверсалей семейства $\varphi =(S_{1} \dts S_{m} )$ непустых подмножеств множества $E=\{ e_{1} \dts e_{n} \}$ состоит в исследовании $(m \times n)$ -матрицы $A=(a_{ij})$ , в которой $a_{ij} =1$ , если $e_{j} \in S_{i}$ , и $a_{ij}=0$ в противном случае. (Любую такую матрицу, все элементы которой равны или , мы называем -матрицей) этого семейства.

Определение словарного ранга. Назовем словарным рангом матрицы наибольшее число единиц в , никакие две из которых не лежат в одной и той же строке или в одном и том же столбце. Тогда $\varphi$ имеет трансверсаль в том и только в том случае, если словарный ранг матрицы равен . Более того, словарный ранг матрицы равен в точности числу элементов частичной трансверсали, обладающей наибольшей возможной мощностью. В качестве второго приложения теоремы Холла рассмотрим известный результат о -матрицах, называемой теоремой Кенига-Эгервари.

Теорема (Кенига-Эгервари, 1931) Словарный ранг -матрицы равен минимальному числу $\mu$ строк и столбцов, которые в совокупности содержат все единицы из .

Замечание В качестве иллюстрации этой теоремы рассмотрим матрицу

$\begin{aligned} & \,\,\,\,\,\begin{matrix} e_{1}\,\, & e_{2}\,\, & e_{3}\,\, & e_{4}\,\, & e_{5}\,\, & e_{6} \end{matrix}\\ \begin{matrix} S_1 \\ S_2 \\ S_3 \\ S_4 \\ S_5 \\ \end{matrix} & \left( \begin{matrix} 1\phantom{1} & 1\phantom{1} & 0\phantom{1} & 0\phantom{1} & 0\phantom{1} & 0\phantom{1}\\ 1\phantom{1} & 1 & 0\phantom{1} & 0\phantom{1} & 0\phantom{1} & 0\phantom{1}\\ 0\phantom{1} & 1\phantom{1} & 1\phantom{1} & 0\phantom{1} & 0\phantom{1} & 0\phantom{1}\\ 0\phantom{1} & 1\phantom{1} & 1\phantom{1} & 0\phantom{1} & 0\phantom{1} & 0\phantom{1}\\ 1\phantom{1} & 0\phantom{1} & 0\phantom{1} & 1\phantom{1} & 1\phantom{1} & 1\phantom{1} \end{matrix} \right)\!, \end{aligned}$

которая является матрицей семейства $\varphi =(S_{1} \dts S_{5}).$ Ясно, что и ее словарный ранг, и число $\mu$ равны четырем.

Доказательство. Очевидно, что словарный ранг не может превосходить числа $\mu$ . Чтобы доказать равенство, можно без потери общности предположить, что все единицы из содержатся в строках и столбцах (где $r+s=\mu$ ) и что строки и столбцы расположены в таком порядке, что в нижнем левом углу матрицы А находится $(m-r)\times (n-s)$ -подматрица, полностью состоящая из нулей.

Если $i\le r$ , то определим $S_{i}$ как множество целых чисел $j\le n-s$ , таких, что $a_{ij} =1$ . Нетрудно проверить, что объединение любых множеств $S_{i}$ содержит по меньшей мере целых чисел; поэтому семейство $\varphi =(S_{1} \dts S_{r})$ имеет трансверсаль. Отсюда следует, что подматрица из содержит множество из единиц, никакие две из которых не принадлежат одной и той же строке или одному и тому же столбцу. Аналогично, матрица содержит множество из единиц, обладающих тем же свойством. Таким образом, матрица содержит множество из единиц, никакие две из которых не принадлежат одной и той же строке или одному и тому же столбцу. Тем самым показано, что $\mu$ не превосходит словарного ранга.

Мы только что доказали теорему Кенига-Эгервари с помощью теоремы Холла, а доказательство теоремы Холла с помощью теоремы Кенига-Эгервари и того проще. Следовательно, эти две теоремы в некотором смысле эквивалентны. В лекции 17 мы докажем теорему о максимальном потоке и минимальном разрезе, которая тоже эквивалентна теореме Холла.

Общие трансверсали. Если — непустое конечное множество, а $\varphi =(S_{1} \dts S_{m})$ и $\tau =(T_{1}\dts T_{m})$ — два семейства его непустых подмножеств, то интересно знать, когда существует общая трансверсаль для $\varphi$ и $\tau$ , то есть множество, состоящее из различных элементов множества и являющееся трансверсалью и для $\varphi$ , и для $\iota$ .

Сформулируем необходимое и достаточное условие для того, чтобы два семейства $\varphi$ и $\tau$ имели общую трансверсаль; заметим, что эта теорема сводится к теореме Холла, если положить $T_{j}-E$ для $1\le j\le m.$

Теорема Пусть — непустое конечное множество, а $\varphi =(S_{1} \dts$ $S_{m})$ и $\tau =(T_{1} \dts T_{m})$ — два семейства его непустых подмножеств. Тогда $\varphi$ и $\tau$ имеют общую трансверсаль в том и только в том случае, если для всех подмножеств и множества $\{1\dts m\}$

$\left|(\bigcup _{i\in A}S_{i} )\bigcap (\bigcup _{j\in B}T_{j} \right|\ge \left|A\right|+\left|B\right|-m.$

Набросок доказательства. Рассмотрим семейство $U=\{ U_{i}\}$ подмножеств множества $E\bigcup \{1\dts m\}$ (считаем, что и $\{1\dts m\}$ не пересекаются), где множеством индексов также является $E\bigcup \{ 1 \dts m\}$ и где $U_{i} =S_{i}$ , если $i\in \{1\dts m\}$ , и $U_{i} =\{ i\} \bigcup \{ i\} \bigcup \{ j:i\in T_{j} \}$ , если $i\in E.$ Нетрудно проверить, что $\varphi$ и $\tau$ имеют общую трансверсаль тогда и только тогда, если семейство имеет трансверсаль. Применяя затем теорему Холла к семейству , получим нужный результат.

Условия, при которых существует общая трансверсаль для трех семейств непустых подмножеств некоторого множества, пока что не известны, и задача нахождения таких условий кажется очень трудной. Многие попытки решения этой задачи используют теорию матроидов; и действительно, некоторые задачи теории трансверсалей становятся почти тривиальными, если рассматривать их с точки зрения теории матроидов.