Паросочетания и свадьбыРезультаты этой главы носят более комбинаторный характер, чем
результаты всех предыдущих глав, хотя они тесно связаны с теорией графов.
Обсудим хорошо известную "теорему о свадьбах", принадлежащую
Филиппу
Холлу, и некоторые приложения этой теоремы, например, построение латинских
квадратов. Теорема Холла о свадьбахТеорема о свадьбах, доказанная Филиппом Холлом в 1935 г., отвечает на
следующий вопрос, известный под названием задачи о свадьбах:
рассмотрим некоторое конечное множество юношей, каждый из которых знаком с
несколькими девушками; спрашивается, при каких условиях можно женить
юношей так, чтобы каждый из них женился на знакомой ему девушке?
(Будем считать, что полигамия не разрешена.) Например, если имеется четверо
юношей 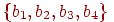 и пять девушек и пять девушек
 , а отношения знакомства между ними показаны в таблице 1,
то возможно следующее решение: , а отношения знакомства между ними показаны в таблице 1,
то возможно следующее решение: 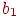 женится
на женится
на  , ,  —
на —
на  , ,  — —  ,
а ,
а  — на — на  . .
Таблица 15.1.
| Юноша | Девушки, с которыми знаком юноша |
|---|
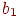 |  |  |  |  |  | | |  |  |  |  |  |  |  | | Эту задачу можно представить графически, взяв двудольный
граф  с множеством вершин, разделенных на два непересекающихся подмножества с множеством вершин, разделенных на два непересекающихся подмножества
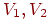 , представляющих юношей и девушек, соответственно,
и соединив ребром каждого юношу со знакомой ему девушкой. , представляющих юношей и девушек, соответственно,
и соединив ребром каждого юношу со знакомой ему девушкой. 
Рис. 15.1.
Напомним определение двудольного графа. Допустим, что множество вершин
графа можно разбить на два непересекающихся подмножества 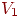 и
и 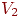 так, что каждое ребро в так, что каждое ребро в  соединяет какую-нибудь вершину
из соединяет какую-нибудь вершину
из 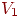 с какой-либо вершиной из с какой-либо вершиной из 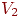 , тогда , тогда  называем
двудольным
графом. Такие графы иногда обозначают называем
двудольным
графом. Такие графы иногда обозначают 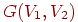 ,
если хотят выделить два указанных подмножества. Двудольный граф можно определить и
по-другому в терминах раскраски его вершин двумя цветами, скажем,
красным и синим. При этом граф называется двудольным, если каждую его
вершину можно окрасить красным или синим цветом так, чтобы любое ребро
имело один конец красный, а другой — синий. Следует подчеркнуть, что
в двудольном графе совсем не обязательно каждая вершина из ,
если хотят выделить два указанных подмножества. Двудольный граф можно определить и
по-другому в терминах раскраски его вершин двумя цветами, скажем,
красным и синим. При этом граф называется двудольным, если каждую его
вершину можно окрасить красным или синим цветом так, чтобы любое ребро
имело один конец красный, а другой — синий. Следует подчеркнуть, что
в двудольном графе совсем не обязательно каждая вершина из 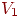 соединена с каждой вершиной из
соединена с каждой вершиной из 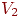 ; если же это так и если при
этом граф ; если же это так и если при
этом граф  , простой, то он называется полным двудольным графом
и обычно обозначается , простой, то он называется полным двудольным графом
и обычно обозначается 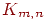 , где , где  —
число вершин, соответственно, в —
число вершин, соответственно, в 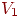 и и 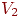 . . Совершенным
паросочетаниемиз 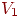 в в 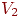 в двудольном графе в двудольном графе 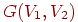 называется взаимно однозначное соответствие между вершинами из
называется взаимно однозначное соответствие между вершинами из 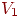 и подмножеством
вершин из и подмножеством
вершин из 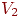 , обладающее тем свойством, что соответствующие вершины
соединены ребром. Ясно, что задачу о свадьбах можно выразить в терминах
теории графов следующим образом: если , обладающее тем свойством, что соответствующие вершины
соединены ребром. Ясно, что задачу о свадьбах можно выразить в терминах
теории графов следующим образом: если  —
двудольный граф, то при каких условиях в —
двудольный граф, то при каких условиях в  существует совершенное
паросочетание из существует совершенное
паросочетание из 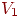 в в 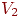 ? ? Используя прежнюю "матримониальную" терминологию, можно
сформулировать следующее очевидное утверждение: необходимое условие для существования решения
в задаче о свадьбах в том, что
любые  юношей из данного множества должны быть
знакомы (в совокупности ), по
меньшей мере, с юношей из данного множества должны быть
знакомы (в совокупности ), по
меньшей мере, с  девушками (для всех целых девушками (для всех целых  , удовлетворяющих
неравенствам , удовлетворяющих
неравенствам 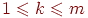 , где через , где через  обозначено общее число юношей).
Необходимость этого условия сразу
вытекает из того, что если оно не верно для какого-нибудь множества
юношей, то мы не сможем женить требуемым способом даже
этих обозначено общее число юношей).
Необходимость этого условия сразу
вытекает из того, что если оно не верно для какого-нибудь множества
юношей, то мы не сможем женить требуемым способом даже
этих  юношей, не говоря уже об остальных. юношей, не говоря уже об остальных. Поразительно, что это очевидное необходимое условие является в то же время
и достаточным. В этом и состоит теорема Холла о свадьбах; ввиду ее
важности мы приведем три доказательства. Первое из них принадлежит Халмошу и Вогену. Теорема (Ф. Холл, 1935)
Решение задачи о свадьбах существует тогда и только тогда,
если любые  юношей из данного множества знакомы в совокупности
по меньшей мере с юношей из данного множества знакомы в совокупности
по меньшей мере с  девушками девушками 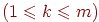 . .
Доказательство Как было отмечено выше, необходимость условия очевидна. Для
доказательства достаточности воспользуемся индукцией и допустим, что
утверждение справедливо, если число юношей меньше  . (Ясно, что
при . (Ясно, что
при 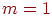 теорема верна.) Предположим теперь, что число юношей
равно теорема верна.) Предположим теперь, что число юношей
равно  , и рассмотрим два возможных случая. , и рассмотрим два возможных случая. (i) Сначала будем считать, что любые  юношей юношей 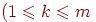 ) в совокупности знакомы по меньшей мере с ) в совокупности знакомы по меньшей мере с  девушками (т.e. что
наше условие всегда выполняется "с одной лишней девушкой"). Тогда, если
взять любого юношу и женить его на любой знакомой ему девушке, для
других девушками (т.e. что
наше условие всегда выполняется "с одной лишней девушкой"). Тогда, если
взять любого юношу и женить его на любой знакомой ему девушке, для
других  юношей останется верным первоначальное условие. По
предположению индукции
мы можем женить этих юношей останется верным первоначальное условие. По
предположению индукции
мы можем женить этих  юношей; тем самым доказательство в первом
случае завершено. юношей; тем самым доказательство в первом
случае завершено. (ii) Предположим теперь, что имеются  юношей юношей 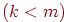 , которые в
совокупности знакомы ровно с , которые в
совокупности знакомы ровно с  девушками. По индуктивному
предположению этих девушками. По индуктивному
предположению этих  юношей можно женить. Остаются
еще юношей можно женить. Остаются
еще  юношей,
но любые юношей,
но любые  из них из них  должны быть знакомы,
по меньшей
мере, с должны быть знакомы,
по меньшей
мере, с  девушками из оставшихся, поскольку в противном случае
эти девушками из оставшихся, поскольку в противном случае
эти  юношей вместе с уже выбранными юношей вместе с уже выбранными  юношами будут
знакомы меньше, чем
с юношами будут
знакомы меньше, чем
с  девушками, а это противоречит нашему предположению.
Следовательно, для этих девушками, а это противоречит нашему предположению.
Следовательно, для этих  юношей выполнено первоначальное
условие, и
по предположению индукции мы можем их женить так, чтобы каждый был
счастлив. Доказательство теоремы закончено. юношей выполнено первоначальное
условие, и
по предположению индукции мы можем их женить так, чтобы каждый был
счастлив. Доказательство теоремы закончено. Теорему Холла можно также сформулировать на языке паросочетаний в
двудольном графе; число элементов множества  обозначается
через обозначается
через  . . Следствие Пусть 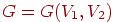 — двудольный граф, и для любого
подмножества — двудольный граф, и для любого
подмножества 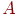 множества множества 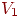 пусть пусть  —
множество тех вершин из —
множество тех вершин из 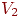 , которые смежны, по крайней мере, с
одной вершиной из , которые смежны, по крайней мере, с
одной вершиной из 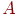 . Тогда совершенное паросочетание
из . Тогда совершенное паросочетание
из 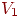 в в 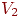 существует в том и только в том случае,
если существует в том и только в том случае,
если 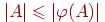 для каждого
подмножества для каждого
подмножества 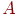 из из 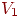 . . Доказательство
Доказательство этого следствия является просто переводом
изложенного выше доказательства на языке теории графов. Приложение теоремы ХоллаРассмотрим приложения теоремы Холла в различных областях. Латинские квадраты
Латинским 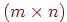 -прямоугольником называется
( -прямоугольником называется
(  )-матрица )-матрица 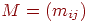 , элементами которой
являются целые числа, удовлетворяющие условиям (1) , элементами которой
являются целые числа, удовлетворяющие условиям (1) 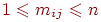 , (2) все
элементы в каждой строке и в каждом столбце различны . Заметим, что из
условий (1) и (2) следует, что , (2) все
элементы в каждой строке и в каждом столбце различны . Заметим, что из
условий (1) и (2) следует, что  ; если ; если  , то
латинский прямоугольник называется латинским квадратом. К примеру, ниже изображены латинский , то
латинский прямоугольник называется латинским квадратом. К примеру, ниже изображены латинский  -прямоугольник и
латинский -прямоугольник и
латинский 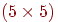 -квадрат. Можно задать следующий вопрос:
если дан латинский -квадрат. Можно задать следующий вопрос:
если дан латинский 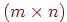 -прямоугольник, где -прямоугольник, где  ,
когда можно присоединить к нему ,
когда можно присоединить к нему  новых строк так, чтобы получился
латинский квадрат? Удивительно, что ответ на этот вопрос "всегда"! новых строк так, чтобы получился
латинский квадрат? Удивительно, что ответ на этот вопрос "всегда"!
![\left[\begin{matrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 1 & 5 & 3\\
3 & 5 & 2 & 1 & 4
\end{matrix}\right]](graphsuse_15_files/a9bf3d33f8ca9a3afff168916fd13d54.png)
Рис. 15.2.
![\left[\begin{matrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 1 & 5 & 3\\
3 & 5 & 2 & 1 & 4\\
4 & 3 & 5 & 2 & 1\\
5 & 1 & 4 & 3 & 2
\end{matrix}\right]](graphsuse_15_files/798fcc55d6c6ead76f6d22766c05a3e5.png)
Рис. 15.3.
Латинские квадраты долгое время были известны лишь математикам и любителям
головоломок и, в основном, благодаря одной знаменитой задаче
Л.Эйлера1) В 1782 г.
Эйлер предложил следующую проблему. Среди 36 офицеров находится по шесть офицеров шести
различных званий из шести полков. Можно ли построить этих офицеров в каре так, чтобы в
каждой колонне и каждой шеренге встречались офицеры всех званий и всех
полков? Лишь в 1901 г. удалось доказать, что это невозможно. Однако связанные с
задачей Эйлера латинские квадраты не потеряли интереса, так как вскоре
обнаружилось, что они имеют многообразные практические применения.
А в конце 60-х годов двадцатого столетия они были применены в теории
кодирования. Получающиеся на их основе коды допускают простые алгоритмы
декодирования.
1)
Леонард Эйлер (1707-1783) — один из великих
математиков XVIII века, создавших основы математического анализа.
Швейцарец по происхождению, он жил и работал преимущественно в России.
Эйлер, выделявшийся своей исключительной интуицией и разносторонностью
интересов, оставил глубокий след практически во всех областях современной
ему математики. Большое количество его замечательных результатов послужило
основой для дальнейшего развития многих разделов математики.
|

![\left[\begin{matrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 1 & 5 & 3\\
3 & 5 & 2 & 1 & 4
\end{matrix}\right]](graphsuse_15_files/a9bf3d33f8ca9a3afff168916fd13d54.png)
![\left[\begin{matrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 1 & 5 & 3\\
3 & 5 & 2 & 1 & 4\\
4 & 3 & 5 & 2 & 1\\
5 & 1 & 4 & 3 & 2
\end{matrix}\right]](graphsuse_15_files/798fcc55d6c6ead76f6d22766c05a3e5.png)