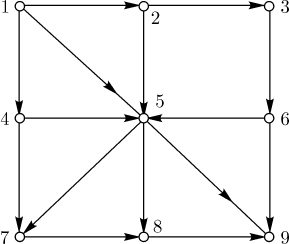
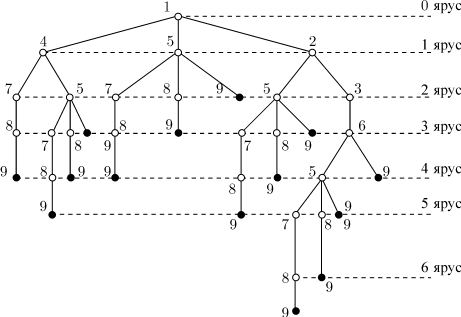
Отыскание кратчайшего пути

На (рис. 13.1) изображена схема местности. Передвигаться из пункта в пункт можно только по стрелкам. В каждом пункте можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого из этих путей наименьшая длина? У какого наибольшая? Ответить на эти вопросы помогают деревья.

Начиная с вершины 1, последовательно "расслаиваем" граф путей в дерево. При этом каждая вершина столько раз получает самостоятельное значение, сколько в нее в первоначальном графе входило путей (рис. 13.2). Наикратчайший путь заканчивается в меньшем "ярусе" висячей вершины дерева, самый длинный путь заканчивается в наибольшем "ярусе" (ярусы отмечены на рисунке штриховыми линиями).

Число путей равно числу висячих вершин дерева, то есть 14. Длина кратчайшего пути (1,5,9) равна 2. Длина наиболее продолжительного пути равна 7. Длину пути помогает определить размещение каждой вершины дерева в соответствующем ярусе.

Этот пример, кстати, показывает, что понятие "длина пути" в теории графов не обязательно совпадает с понятием "длина пути" в геометрии или географии.

Рисунок дерева полезен не только тем, что позволяет подсчитать число всех возможных путей, отыскать среди них кратчайший и наиболее протяженный. Он позволяет еще одновременно "увидеть" все пути и сравнить их.

Рис. 13.1. 

Рис. 13.2. 

Вероятность и генетика

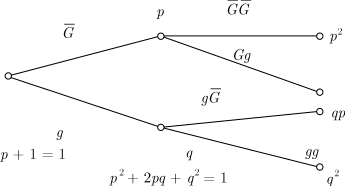
Приведем примеры использования деревьев в генетике. С помощью дерева можно наглядно представить наследование пары генов и , передаваемых родителями. Потомок получает эти гены в одной из комбинаций: или . Генетически комбинация не отличается от комбинации .

В генетике допускается, что наследование данного гена происходит случайно, независимо и с равными вероятностями для всех потомков (у растений, например, их может быть очень много). Пусть ген наследуется (и от отца, и от матери) с вероятностью , ген — с вероятностью . В этом случае отца в смысле унаследования гена можно уподобить, например, одной бросаемой монете, мать — второй (рис. 13.3). Тогда .

Рис. 13.3. 

Далее будем полагать, что . Заметим, что у таких "генеалогических" деревьев вершины, если они не висячие и не корневые, имеют степень 3.

Теперь от родителей перейдем к "дедушкам" и "бабушкам" и продлим дерево еще на один ярус.

Когда сочетаются браком двоюродные брат и сестра, они могут передать своему ребенку копии пар генов, которыми обладали их общие дедушка и бабушка (возможными мутациями этих генов пренебрегаем).

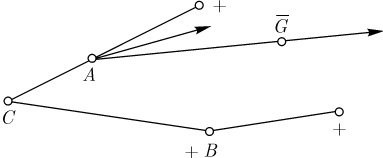
Считая, что в общем случае неизвестно численное значение вероятности того, что потомок наследует от своих родителей пару одинаковых генов или , определим в зависимости от вероятность унаследования общей пары генов от общего дедушки.

Граф, описывающий ситуацию, которая нас интересует, в случаях так называемого кровного родства деревом не является — две его висячие вершины "слипаются" (рис. 13.4).

Рис. 13.4. 

Введем коэффициент кровного родства по формуле , где — вероятность того, что оба гена являются копиями генов . При этом оказывается, что вероятность нетрудно подсчитать.

Рассмотрим один из генов, который унаследовал от своего отца . Вероятность того, что унаследовал этот ген от своего деда , равна . Вероятность того, что дедушка передал копию того же гена , также равна , и вероятность того, что передал копию этого гена , равна . Все эти события независимые, и, следовательно, .

Рассмотренный пример дает некоторое представление о расчетах, связанных с проблемами сохранения в потомстве желательных признаков прародителей: вывода сортов пшеницы, пород собак, голубей, домашних животных, искусственного восстановления вымирающих пород животных. Все эти проблемы разные по роли и значимости, но они имеют общую математическую суть.