INTUIT.ru::Интернет-Университет Информационных Технологий

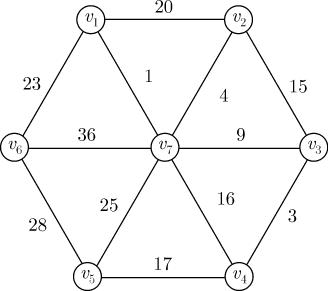
Оптимальным каркасом взвешенного графа называется каркас, минимизирующий некоторую функцию от весов входящих в него ребер. Чаще всего в качестве такой функции выступает сумма весов ребер, реже — произведение. Оптимальный каркас еще называют кратчайшей связывающей сетью для данного графа.

Задача о построении кратчайшей связывающей сети встречается в различных приложениях достаточно часто.

Нахождение каркасов в графе

Алгоритм нахождения каркаса на основе поиска в глубину.

Вход.	Связный граф  , заданный списками смежности ЗАПИСЬ  
Выход.	Каркас   графа .
Процедура	WGD ( : граф;  : вершина)
//поиск в глубину, с нахождением ребер дерева; переменные НОВЫЙ, ЗАПИСЬ,   — глобальные//
Шаг 1. 	НОВЫЙ ;
Шаг 2. 	Для  (ЗАПИСЬ  цикл
Шаг 3. 	если НОВЫЙ[ ] то //  — новое ребро//
Шаг 4.	;
Шаг 5.	;
   все
все;
Шаг 6.	Начало //главная программа//
Шаг 7.	Для   цикл НОВЫЙ ;
Шаг 8.	 //множество найденных к этому моменту ребер//
Шаг 9.	; //  — произвольная вершина графа//
   все
конец.

Алгоритм нахождения каркаса на основе поиска в ширину.

Вход.	Связный граф  , представленный списками смежности ЗАПИСЬ ,  .
Выход.	Каркас   графа .
Процедура	КАРКАС( : граф;  : вершина)
Шаг 1.	для   цикл НОВЫЙ[u]=истина все; //инициализация//
Шаг 2.	; // — множество найденных к этому моменту ребер//
Шаг 3.	ОЧЕРЕДЬ ; ОЧЕРЕДЬ  ; //корень каркаса//
Шаг 4.	НОВЫЙ ;
Шаг 5.	Пока ОЧЕРЕДЬ  цикл
Шаг 6.	 ОЧЕРЕДЬ;
Шаг 7.	Для  ЗАПИСЬ  цикл
Шаг 8.	если НОВЫЙ  то //  — новое ребро//
Шаг 9.	ОЧЕРЕДЬ  ;
Шаг 10.	НОВЫЙ ;
Шаг 11.	
         все
      все
   все
все.

Алгоритм Краскала

Вход.	Неориентированный граф   с функцией стоимости ребер .
Выход.	Оптимальный каркас  .
Метод
Процедура Оптимальный каркас ( : граф)  
Шаг 1.	
Шаг 2.	
Шаг 3.	Построить очередь с приоритетами  , содержащую все ребра из ;
Шаг 4.	Для всех   из   цикла  добавить  к  все;
Шаг 5.	Пока   цикл
Шаг 6.	Выбрать в   ребро   наименьшей стоимости;
Шаг 7.	удалить ( )  из ;
Шаг 8.	Если   и  принадлежат различным множествам   и  из 
Шаг 9.	То заменить   и   на   в :
Шаг 10.	добавить   к 
      все
   все
все.

Ребро	Стоимость
$(v_{1},v_{7})$	1
$(v_{3},v_{4})$	3
$(v_{2},v_{1})$	4
$(v_{3},v_{1})$	9
$(v_{2},v_{3})$	15
$(v_{4},v_{7})$	16
$(v_{1},v_{5})$	17
$(v_{1},v_{2})$	20
$(v_{1},v_{6})$	23
$(v_{5},v_{7})$	25
$(v_{5},v_{6})$	28
$(v_{6},v_{7})$	36

Для графа, приведенного на (рис.12.1), оптимальным каркасом будет — это можно проверить самостоятельно.

Изоморфизм деревьев

Два графа

изоморфны (записывается $G \cong H$ или иногда

), если между множествами вершин существует взаимно однозначное соответствие, сохраняющее смежность.

Инвариант графа

— это число, связанное с

, которое принимает одно и то же значение на любом графе, изоморфном

. Полный набор инвариантов определяет граф с точностью до изоморфизма.

Пусть дерево

и его

инцидентор, т.е. предикат, равный единице в том и только в том случае, когда ребро

инцидентно вершинам

Дерево

называется изоморфным дереву ${T}_2=(V_2,E_2$ ), если между вершинами деревьев, а также между их ребрами можно установить взаимно однозначное соответствие $V_1 \Leftrightarrow V_2$ и $E_1 \Leftrightarrow E_2$ , сохраняющее инцидентор, т.е. такое, что $(\forall v,w \in V_1)$ $(\forall v',w' \in V_2$ $(\forall e \in E_1)$ $(\forall e' \in E_2)$ ( $v \Leftrightarrow v'$ $\&$ $w \Leftrightarrow w'$ $\&$ $e \Leftrightarrow e' \Rightarrow [P_1(e,v,w)] = P_2(e',v',w')$ ).

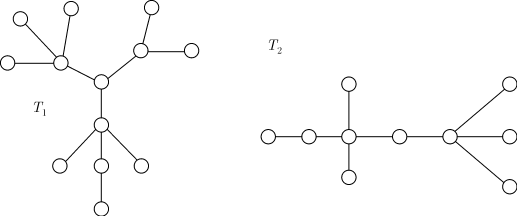
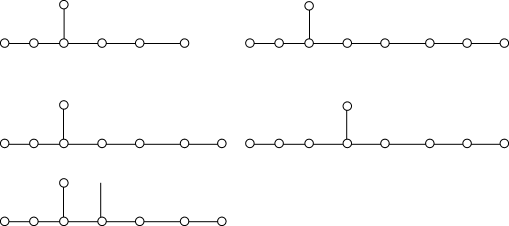
Другими словами, два дерева изоморфны, если между их вершинами можно установить взаимно однозначное соответствие, сохраняющее отношение инцидентности (смежности).

Отношение деревьев рефлексивно, симметрично, транзитивно, , т.е. представляет собой транзитивность. Матрицы смежности изоморфных деревьев могут быть переведены одна в другую перестановкой рядов, т.е. одновременной одинаковой перестановкой строк и столбцов.

Пример изоморфных деревьев: нетрудно заметить, что они отличаются лишь способом представления (например, способом изображения на плоскости).

Два корневых дерева называются изоморфными, если существует взаимно однозначная функция, которая отображает множество вершин одного дерева на множество другого и не только сохраняет смежность, но и переводит корень одного дерева в корень другого.

Изоморфное отображение дерева

на себя называется автоморфизмом дерева. Совокупность всех автоморфизмов дерева

, обозначаемая $\Gamma(T)$ , образует группу, называемую группой дерева

. Таким образом, элементы группы $\Gamma(T)$ являются подстановками, действующими на множестве вершин

. Порядок

группы $\Gamma(T)$ есть число симметрий дерева

Дерево

называется асимметричным, если его группа автоморфизмов есть единичная группа, т.е.

Примеры асимметричных деревьев порядка 7, 8, 9.

Два плоских дерева называются изоморфными, если существует гомеоморфное отображение плоскости на себя, сохраняющее ориентацию, и такое, что отображает одно из этих деревьев в другое.

Два помеченных дерева называются изоморфными, если существует взаимно однозначная функция, отображающая множество вершин одного дерева на множество вершин другого, которая не только сохраняет смежность, но и переводит вершину с меткой в вершину с той же меткой.

Каркас неориентированного графа

Нахождение каркасов в графе

Алгоритм Краскала

Изоморфизм деревьев