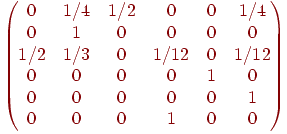Еще раз об ориентированных графахСтепенью
выхода вершины  ориентированного графа называется
число выходящих из ориентированного графа называется
число выходящих из  дуг (ребер). Степенью входа
вершины дуг (ребер). Степенью входа
вершины  ориентированного графа называется число входящих
в ориентированного графа называется число входящих
в  дуг (ребер). дуг (ребер).
Изолированной вершиной называется вершина, у которой и степень
входа, и степень выхода равны  . Источникомназывается вершина,
степень выхода которой положительна, а степень входа равна . Источникомназывается вершина,
степень выхода которой положительна, а степень входа равна  .
Стоком называется вершина, степень входа которой положительна,
а степень выхода равна .
Стоком называется вершина, степень входа которой положительна,
а степень выхода равна  .
Путем в ориентированном графе .
Путем в ориентированном графе  от от  до
до  называется последовательность ориентированных дуг
(ребер) называется последовательность ориентированных дуг
(ребер)  , , 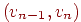 ,
такая, что конец каждой предыдущей дуги (ребра) совпадает с началом следующей и ни одна дуга
(ребро) не встречается более одного раза. Если в ориентированном
графе ,
такая, что конец каждой предыдущей дуги (ребра) совпадает с началом следующей и ни одна дуга
(ребро) не встречается более одного раза. Если в ориентированном
графе  нашелся путь от нашелся путь от  до до  , то обратного пути
от , то обратного пути
от  к к  может и не быть. Простым путем в ориентированном графе
называется путь, в котором ни одна вершина не содержится более одного
раза.
Замкнутый путь в ориентированном графе называется
ориентированным циклом. Длиной пути называется число дуг (ребер) в
этом пути. Расстоянием от может и не быть. Простым путем в ориентированном графе
называется путь, в котором ни одна вершина не содержится более одного
раза.
Замкнутый путь в ориентированном графе называется
ориентированным циклом. Длиной пути называется число дуг (ребер) в
этом пути. Расстоянием от  до до  в
ориентированном графе называется длина наикратчайшего пути от в
ориентированном графе называется длина наикратчайшего пути от  до
до  . Если пути
от . Если пути
от  до до  не существует, торасстояние
от не существует, торасстояние
от  до до  называется
бесконечным. Оно
обозначается называется
бесконечным. Оно
обозначается  . Расстояние от . Расстояние от  до
до  будем обозначать будем обозначать  . Полным ориентированным
графом называется граф, каждая пара вершин которого соединена в точности одной
ориентированной дугой (ребром). Если с каждого ребра (дуги) полного
ориентированного графа снять направление, то образуется полный граф с
неориентированными ребрами (дугами). . Полным ориентированным
графом называется граф, каждая пара вершин которого соединена в точности одной
ориентированной дугой (ребром). Если с каждого ребра (дуги) полного
ориентированного графа снять направление, то образуется полный граф с
неориентированными ребрами (дугами). Задачи на круговые бескомпромиссные турнирыНапомним, что соревнование, в котором каждая из команд играет с каждой из
остальных команд в точности по одному разу, называют круговым
турниром или турниром в один круг. Если каждая встреча
оканчивается непременно выигрышем одной из команд, то круговой
турнир называется бескомпромиссным. Круговой бескомпромиссный
турнир проводится, например, в волейболе и баскетболе. Так как мы
рассматриваем исключительно бескомпромиссные круговые турниры, не
возникает опасности спутать их с каким-либо другим видом турниров; такое
соревнование будем называть сокращенно турниром. Каждому турниру
соответствует полный ориентированный граф, в котором вершины представляют
команды, а каждая ориентированная дуга  выражает
отношение " выражает
отношение "  победила победила  ".
Степень выхода любой вершины ".
Степень выхода любой вершины  есть число побед, одержанных
командой есть число побед, одержанных
командой  . .
Задача 1. Турнир по волейболу
проводится между  командами.
Докажем, что если какие-нибудь две команды одержали в турнире одинаковое
число побед, то найдутся среди участников три команды I, II, III, такие,
что I выиграла у II, II выиграла у III, а III выиграла у I. командами.
Докажем, что если какие-нибудь две команды одержали в турнире одинаковое
число побед, то найдутся среди участников три команды I, II, III, такие,
что I выиграла у II, II выиграла у III, а III выиграла у I. Решение. Пусть  и и  — две команды, одержавшие
одинаковое число побед, например, — две команды, одержавшие
одинаковое число побед, например, 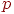 побед. Пусть к тому
же побед. Пусть к тому
же  выиграла у
выиграла у  . Те . Те 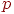 команд, у которых выиграла
команда команд, у которых выиграла
команда  ,
обозначим ,
обозначим  (рис. 10.1). (рис. 10.1). 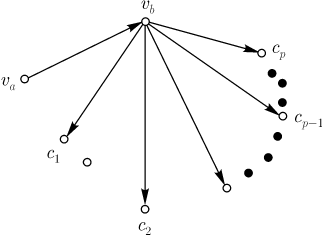
Рис. 10.1.
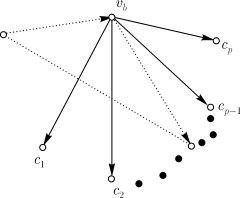
Рис. 10.2.
Команда  не могла одержать победы над всеми командами из
числа не могла одержать победы над всеми командами из
числа  , так как иначе она одержала бы больше,
чем , так как иначе она одержала бы больше,
чем 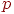 побед. побед. Следовательно, среди команд  найдется
хотя бы одна, которая одержала победу над найдется
хотя бы одна, которая одержала победу над  . Стрелку от нее
направим . Стрелку от нее
направим  . Путь замкнется. . Путь замкнется. Сформулируем полученный результат на языке графов. Теорема 10.1.
Если в полном ориентированном графе с  вершинами хотя бы две
вершины имеют одинаковые степени выхода, то в этом ориентированном графе найдутся вершинами хотя бы две
вершины имеют одинаковые степени выхода, то в этом ориентированном графе найдутся
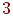 такие вершины, что дуги (ребра), соединяющие их, образуют
ориентированный цикл. такие вершины, что дуги (ребра), соединяющие их, образуют
ориентированный цикл.
Задача 2. Турнир между  шахматистами закончился без ничьих. Можно
ли пронумеровать всех участников в таком порядке, чтобы оказалось, что
каждый выиграл партию у шахматиста, имеющего номер на единицу больше? шахматистами закончился без ничьих. Можно
ли пронумеровать всех участников в таком порядке, чтобы оказалось, что
каждый выиграл партию у шахматиста, имеющего номер на единицу больше? Решение. Достаточно выяснить, что всякий полный ориентированный граф
с  вершинами имеет простой путь, проходящий через все вершины
орграфа. Доказательство: проведем методом математической индукции по числу вершин
орграфа. вершинами имеет простой путь, проходящий через все вершины
орграфа. Доказательство: проведем методом математической индукции по числу вершин
орграфа. Для  утверждение верно. Теперь предположим, что в любом
полном орграфе утверждение верно. Теперь предположим, что в любом
полном орграфе  с с  вершинами найдется простой путь,
проходящий через все вершины графа. Обозначим его вершинами найдется простой путь,
проходящий через все вершины графа. Обозначим его 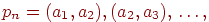
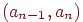 . Добавим теперь произвольную
вершину . Добавим теперь произвольную
вершину  и ребра
(дуги), соединяющие ее со всеми остальными вершинами
орграфа и ребра
(дуги), соединяющие ее со всеми остальными вершинами
орграфа  . . Если ребро (дуга), соединяющее  и и  ,
направлено от ,
направлено от  к
к  , то пройден путь , то пройден путь  до
до  (рис. 10.3).
Если ребро (дуга) направлено от (рис. 10.3).
Если ребро (дуга) направлено от  к к  , то
рассмотрим последовательность ребер (дуг), соединяющих , то
рассмотрим последовательность ребер (дуг), соединяющих  с с
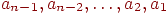 . Если все ребра (дуги) направлены
от . Если все ребра (дуги) направлены
от
 , то к пути , то к пути  можно добавить ребро можно добавить ребро
 . . Если они все выходят из  , то возьмем первое ребро
(дугу) этой последовательности, входящее в , то возьмем первое ребро
(дугу) этой последовательности, входящее в  . Пусть это будет ребро
(дуга) . Пусть это будет ребро
(дуга)  (рис. 10.4). (рис. 10.4). Прервем путь  в в 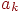 и продолжим его по
ребрам (дугам) и продолжим его по
ребрам (дугам)
 , , 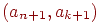 , после чего вновь
вернемся к прежнему
маршруту, то есть искомый путь будет следующим: , после чего вновь
вернемся к прежнему
маршруту, то есть искомый путь будет следующим:  , , 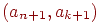 , ,
 , ,
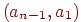 По принципу математической индукции утверждение верно для всякого
натурального  . . А коль есть такой путь в графе, следовательно, всех игроков можно будет
пронумеровать так, чтобы оказалось, что каждый выиграл партию
у шахматиста, имеющего номер на единицу меньше. 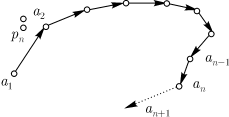
Рис. 10.3.
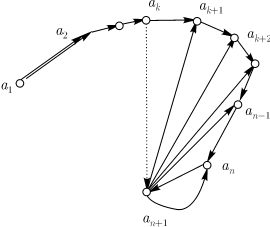
Рис. 10.4.
Полученный результат сформулируем в виде теоремы. Теорема 10.2.
Всякий полный орграф с  вершинами имеет простой ориентированный
путь, проходящий через все вершины орграфа. вершинами имеет простой ориентированный
путь, проходящий через все вершины орграфа.
Цепи МарковаОрграфы возникают во многих жизненных ситуациях. Не пытаясь охватить
большое число таких ситуаций, ограничимся рассмотрением одной из них.
Интересующихся данными приложениями отошлем к главе 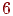 книги
Басакера и Саати "Конечные графы и сети".М.: Наука. 1974. книги
Басакера и Саати "Конечные графы и сети".М.: Наука. 1974. Задача, которую мы рассмотрим, интересна сама по себе, а отчасти
рассматриваем мы ее из-за того, что ее изложение не требует введения
большого количества новых терминов. Рассмотрим задачу об осле, стоящем точно между двумя копнами: соломы ржи и
соломы пшеницы (рис. 10.5). Осел стоит между двумя копнами: "Рожь" и "Пшеница"
(рис. 10.5). Каждую минуту он либо передвигается на десять метров в сторону первой копны
(с вероятностью 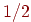 ), либо в сторону второй копны (с
вероятностью ), либо в сторону второй копны (с
вероятностью 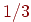 ), либо остается там, где стоял (с вероятностью ), либо остается там, где стоял (с вероятностью
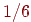 ); такое поведение называется одномерным случайным блужданием . Будем
предполагать, что обе копны являются "поглощающими" в том смысле,
что если осел подойдет к одной из копен, то он там и останется. Зная
расстояние между двумя копнами и начальное положение осла, можно поставить
несколько вопросов, например: у какой копны он очутится с большей
вероятностью и какое наиболее вероятное время ему понадобится, чтобы
попасть туда? ); такое поведение называется одномерным случайным блужданием . Будем
предполагать, что обе копны являются "поглощающими" в том смысле,
что если осел подойдет к одной из копен, то он там и останется. Зная
расстояние между двумя копнами и начальное положение осла, можно поставить
несколько вопросов, например: у какой копны он очутится с большей
вероятностью и какое наиболее вероятное время ему понадобится, чтобы
попасть туда? 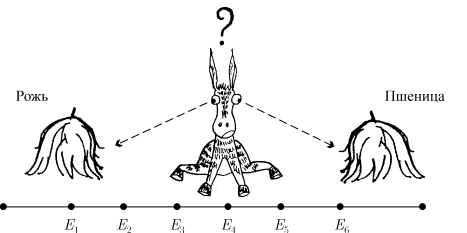
Рис. 10.5.
Чтобы исследовать эту задачу подробнее, предположим, что расстояние между
копнами равно пятидесяти метрам и что наш осел находится в двадцати метрах
от копны "Пшеницы". Если места, где можно остановиться, обозначить
через  ( ( 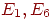 — сами
копны), то его начальное положение — сами
копны), то его начальное положение  можно задать вектором можно задать вектором
 , ,  -я
компонента которого равна вероятности того, что он первоначально находится
в -я
компонента которого равна вероятности того, что он первоначально находится
в  . Далее, по прошествии одной минуты вероятности его
местоположения описываются вектором . Далее, по прошествии одной минуты вероятности его
местоположения описываются вектором 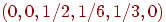 , а через
две минуты — вектором , а через
две минуты — вектором 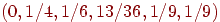 . Ясно, что
непосредственное вычисление вероятности его нахождения в заданном месте по
прошествии . Ясно, что
непосредственное вычисление вероятности его нахождения в заданном месте по
прошествии  минут становится затруднительным. Оказалось, что
удобнее всего ввести для этого матрицу перехода. минут становится затруднительным. Оказалось, что
удобнее всего ввести для этого матрицу перехода.

Рис. 10.6.
Пусть  — вероятность того, что он переместится
из — вероятность того, что он переместится
из  в в 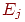 за одну минуту. Например, за одну минуту. Например,  и
и 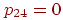 .
Эти вероятности .
Эти вероятности  называются вероятностями перехода,
а называются вероятностями перехода,
а  -матрицу -матрицу 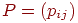 называют матрицей
перехода (рис. 10.6). Заметим, что каждый элемент
матрицы называют матрицей
перехода (рис. 10.6). Заметим, что каждый элемент
матрицы  неотрицателен и что сумма элементов любой из строк равна единице. Из всего
этого следует, что неотрицателен и что сумма элементов любой из строк равна единице. Из всего
этого следует, что  — начальный вектор-строка,
определенный выше, местоположение осла по прошествии одной минуты описывается
вектором-строкой — начальный вектор-строка,
определенный выше, местоположение осла по прошествии одной минуты описывается
вектором-строкой  , а после , а после  минут —
вектором минут —
вектором  . Другими
словами, . Другими
словами,  -я компонента вектора -я компонента вектора  определяет
вероятность того,
что по истечении определяет
вероятность того,
что по истечении  минут осел оказался в минут осел оказался в  . . Можно обобщить эти понятия. Назовем вектором вероятностей
вектор-строку, все компоненты которого неотрицательны и дают в сумме
единицу. Тогда матрица перехода определяется как квадратная
матрица, в которой каждая строка является вектором вероятностей. Теперь
можно определить цепь Маркова (или просто цепь) как пару 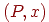 ,
где ,
где  есть есть  -матрица перехода, а -матрица перехода, а  есть есть
 -вектор-строка. Если каждый элемент -вектор-строка. Если каждый элемент  из
из  рассматривать как
вероятность перехода из позиции рассматривать как
вероятность перехода из позиции  в позицию
в позицию 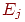 , а , а  — как
начальный вектор вероятностей, то придем к классическому понятию
дискретной стационарной цепи Маркова, которое можно найти в книгах
по теории вероятностей (см. Феллер В. Введение в теорию вероятностей и ее
приложения. Т.1. М.: Мир. 1967) Позиция — как
начальный вектор вероятностей, то придем к классическому понятию
дискретной стационарной цепи Маркова, которое можно найти в книгах
по теории вероятностей (см. Феллер В. Введение в теорию вероятностей и ее
приложения. Т.1. М.: Мир. 1967) Позиция  обычно называется
состоянием
цепи. Опишем различные способы их классификации. обычно называется
состоянием
цепи. Опишем различные способы их классификации. Нас будет интересовать следующее: можно ли попасть из одного данного
состояния в другое, и если да, то за какое наименьшее время. Например, в
задаче об осле из  в в  можно попасть за
три минуты и вообще нельзя попасть из можно попасть за
три минуты и вообще нельзя попасть из  в в  . Следовательно,
в основном мы будем интересоваться не самими вероятностями . Следовательно,
в основном мы будем интересоваться не самими вероятностями  , а тем,
положительны они или нет. Тогда появляется надежда, что все эти данные удастся представить
в виде орграфа, вершины которого соответствуют состояниям, а дуги
указывают на то, можно ли перейти из одного состояния в другое за одну
минуту. Более точно, если каждое состояние , а тем,
положительны они или нет. Тогда появляется надежда, что все эти данные удастся представить
в виде орграфа, вершины которого соответствуют состояниям, а дуги
указывают на то, можно ли перейти из одного состояния в другое за одну
минуту. Более точно, если каждое состояние  представлено
соответствующей ему вершиной представлено
соответствующей ему вершиной  , то, проводя
из , то, проводя
из  в в  для тех и только тех вершин, для которых
для тех и только тех вершин, для которых 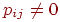 , мы и
получим требуемый орграф. Кроме того, этот орграф можно определить при помощи его
матрицы смежности, если заменить каждый ненулевой элемент
матрицы , мы и
получим требуемый орграф. Кроме того, этот орграф можно определить при помощи его
матрицы смежности, если заменить каждый ненулевой элемент
матрицы  на
единицу. Мы будем называть этот орграф ассоциированным орграфом
данной цепи Маркова. Ассоциированный орграф одномерного случайного
блуждания, связанного с задачей об осле, изображен на (рис. 10.7). на
единицу. Мы будем называть этот орграф ассоциированным орграфом
данной цепи Маркова. Ассоциированный орграф одномерного случайного
блуждания, связанного с задачей об осле, изображен на (рис. 10.7). Другой пример: если цепь Маркова имеет матрицу перехода, приведенную на рис. 10.8, то ассоциированный орграф этой цепи выглядит так, как показано на
(рис. 10.9). 
Рис. 10.7.
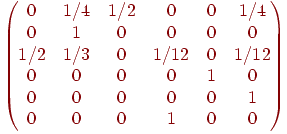
Рис. 10.8.
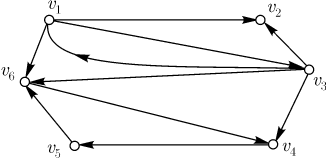
Рис. 10.9.
Теперь ясно, что в цепи Маркова из состояния  в
состояние в
состояние
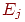 можно попасть в том и только в том случае, если в
ассоциированном
орграфе существует орцепь из можно попасть в том и только в том случае, если в
ассоциированном
орграфе существует орцепь из  в в  , и что
наименьшее
возможное время попадания равно длине кратчайшей из таких орцепей. Цепь
Маркова, в которой из любого состояния можно попасть в любое другое,
называется
неприводимой. Ясно, что цепь Маркова неприводима тогда и
только тогда, если ее ассоциированный орграф сильно связан. Заметим,
что ни одна из описанных выше цепей не является неприводимой. , и что
наименьшее
возможное время попадания равно длине кратчайшей из таких орцепей. Цепь
Маркова, в которой из любого состояния можно попасть в любое другое,
называется
неприводимой. Ясно, что цепь Маркова неприводима тогда и
только тогда, если ее ассоциированный орграф сильно связан. Заметим,
что ни одна из описанных выше цепей не является неприводимой. При дальнейших исследованиях принято различать те состояния, в которые мы
продолжаем возвращаться независимо от продолжительности процесса, и те,
в которые мы попадаем несколько раз и никогда не возвращаемся. Более точно
это выглядит так: если начальное состояние есть  и вероятность возвращения в
и вероятность возвращения в  на некотором более позднем шаге равна единице,
то на некотором более позднем шаге равна единице,
то  называется возвратным (или рекурсивным)
состоянием. В противном случае
состояние называется возвратным (или рекурсивным)
состоянием. В противном случае
состояние  называется
невозвратным. В задаче об осле, например, очевидно, что состояния называется
невозвратным. В задаче об осле, например, очевидно, что состояния
 и и  являются возвратными, тогда как все
другие состояния — невозвратными. В более сложных примерах вычисление нужных
вероятностей становится очень хитрым делом, и поэтому проще бывает
классифицировать состояния, анализируя ассоциированный орграф цепи.
Нетрудно понять, что состояние являются возвратными, тогда как все
другие состояния — невозвратными. В более сложных примерах вычисление нужных
вероятностей становится очень хитрым делом, и поэтому проще бывает
классифицировать состояния, анализируя ассоциированный орграф цепи.
Нетрудно понять, что состояние  возвратно тогда и только
тогда, если существование простой орцепи из возвратно тогда и только
тогда, если существование простой орцепи из  в в  в ассоциированном орграфе влечет за собой существование простой орцепи из
в ассоциированном орграфе влечет за собой существование простой орцепи из  в
в  .
В орграфе, изображенном на (рис. 10.7), существует простая орцепь из .
В орграфе, изображенном на (рис. 10.7), существует простая орцепь из
 в в  , но нет ни одной орцепи из , но нет ни одной орцепи из  в
в  . Следовательно,
состояния . Следовательно,
состояния  и, аналогично, и, аналогично,  невозвратны
( невозвратны
( 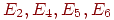 возвратны). Состояние (такое, как возвратны). Состояние (такое, как
 ), из которого нельзя попасть ни в какое другое, называется поглощающим состоянием. ), из которого нельзя попасть ни в какое другое, называется поглощающим состоянием. Другой прием классификации состояний опирается на понятие периодичности
состояний.
Состояние  цепи Маркова называется
периодическим с периодом цепи Маркова называется
периодическим с периодом 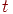 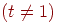 , если
в , если
в  можно вернуться
только по истечении времени, кратного можно вернуться
только по истечении времени, кратного 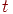 . Если
такого . Если
такого 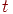 не существует, то состояние не существует, то состояние  называется непериодическим.
Очевидно, что каждое состояние называется непериодическим.
Очевидно, что каждое состояние  , для которого , для которого  , непериодическое. Следовательно, каждое поглощающее состояние —
непериодическое. В задаче об осле не только поглощающее
состояние , непериодическое. Следовательно, каждое поглощающее состояние —
непериодическое. В задаче об осле не только поглощающее
состояние 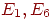 , но и все остальные являются
непериодическими. С другой стороны, во втором примере (рис. 10.7) поглощающее
состояние , но и все остальные являются
непериодическими. С другой стороны, во втором примере (рис. 10.7) поглощающее
состояние  — единственное непериодическое состояние,
поскольку — единственное непериодическое состояние,
поскольку 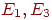 имеют период два, а имеют период два, а  — период три. Используя терминологию орграфов, легко показать, что
состояние
— период три. Используя терминологию орграфов, легко показать, что
состояние  является периодическим с периодом
является периодическим с периодом 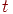 тогда и только тогда, если
в ассоциированном орграфе длина каждой замкнутой орцепи, проходящей
через тогда и только тогда, если
в ассоциированном орграфе длина каждой замкнутой орцепи, проходящей
через  , кратна , кратна 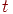 . . И, наконец, для полноты изложения введем еще одно понятие: назовем
состояние цепи Маркова эргодическим, если оно одновременно
возвратно и непериодично. Если любое состояние цепи Маркова является
эргодическим, то назовем ее эргодической цепью.
|